09 Aug

SLAM simulation with sliding window scheme

Tsang-Kai Chang

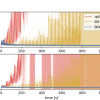
We simulate the BOEM algorithm against two other offline algorithms. Since these two algorithms requires a long time, we simulated them with sliding windows. In the first scenario, the block size of BOEM started with 9 sec, and grows geometrically. The sliding windows for both EM and optimizati...

15 Jul

BOEM SLAM simulation of expanding window

Tsang-Kai Chang

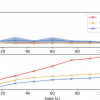
We simulation these SLAM algorithms with increasing duration. We can see that the estimation accuracy is comparable among 3 SLAM algorithms, but the processing times are different. The processing time is basically dominated by the optimization problem. The bigger the optimization problem, the long...

10 Jun

The simulation of BOEM SLAM algorithm

Tsang-Kai Chang

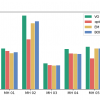
Following up with Alexie's post last week, we furthermore show that the simulation of BOEM SLAM algorithm for 1000 sec. The result is the average of 5 trials. The computation times for other algorithm, including optimization based and the EM SLAM, are too large for 1000 sec, but we have the comparis...

03 Jun

SLAM performance on EuRoC datasets

Tsang-Kai Chang

We compare 3 different SLAM algorithms on EuRoC datasets. As for estimation accuracy, we can see that all SLAM algorithms can improve the accuracy upon the visual-inertial odometry VIO output. The optimization SLAM has the most consistent result, while all SLAM algorithms have comparable perform...

07 May

Tests on the modules of optimization problems

Tsang-Kai Chang

The optimization based SLAM formulate the optimization problem with two kinds of constraints. First, the pre-integrated IMU error establishes the constraints between two spatial states, or two poses. The other one is the reprojection error that links a spatial state and a landmark. In the optimizati...

11 Feb

[Slides] Big picture : Information-Theoretical Semantic SLAM

Zida Wu

Next task: The urgent tests need to be carried out is to find the real pose estimation result only by landmark points without uncertainty evaluate the influence of uncertainty to find the pose estimation effect based on probability map of features After that we can then to test the EM alg...

13 Dec

Test results of IMU error function

Zida Wu

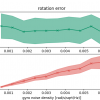
Purpose This blog is to pose optimization results of the IMU erro function in Tsangkai's project. In this test, I try to use simulation data to test the "imu_error" function to examine whether the code is right or not to perform optimization function. Input and output There are two tests. ...

01 Nov

Paper Reivew and Insufficiency of EM Semantic SLAM

Zida Wu

The main paper we reviewed is the Probabilistic Data Association for Semantic SLAM It depicts a promising vista about the probablistic semantic slam. Primarily proposed an EM mathematical framework to consider the detection probabilistic, and using iterative multiply probability way to bring in f...

30 Sep

visual imu landmark data simulation

Zida Wu

gitlablink Frame Introduction Body frame: IMU Coordinate Cam frame: Camera Coordinate World frame: The firt frame of IMU frames Navigation frame: ENU \((0,0,-9.81)\) Core Idea 1. Essential Members in IMU and Camera: imu_acc/imu_acc_bias/acc_noise_sigma/acc_bias_...

  • «
  • »

Search

Popular Tags

foray origami robots blimp ducky vr edg SLAM computer vision computational design roco slam Origami rocolib arduino RoCo design Robot Compiler simulation Motion Planning autonomy edg-model mesh reinforcement learning; multi-agent; mean-field; logics create; kalman filter; motors imu friction mesh network tank esp32 networking contacts multi-agent pushing auxetic machine learning dynamics esp now visual processing wireless control communication webapp pcbs structure ROCO i2c path planning cars Robotica reinforcement learning computer skill openmv test motor dataset visual DARPA odometry Battery surface structure power consumption dash port-arrays modeling origami paper frequency diversity semantic infrastructure auxetics feedback gondola machine vision Consensus bistable auxetic controller gestural intuition mixed reality unit cell robot crawler gestural interface open house network create; kalman filter; EM; refactoring 4-wheeled darpa; create; icra2021 apriltags lidar logic control FORAY perception Quantum Information crazyflie 433mhz optimization propeller Foray structures sensors environmental design radio DER Kullback-Leibler Divergence lasercutter tutorial von Mises Fisher Distribution IR simulink legs project management localization distributed optimization blynk Auxetics painlessmesh experiment results offline reinforcement learning exam research proposal altimeter thrust PCB sensor fusion gate or webots multi-agent path planning UAV RL integration test arnhold joystick balloon test vision processing pushing problem modeling contacts mesh networking motor configuration nodemcu swarm object detection fusionbot ros2 rviz2 gazebo conference matlab arduino nano decentralized surfaces keyboard IROS Integrated Demo throughput peripheral device paper review reinforcement learning; motorized boats Writing slam; paper review rhino Short Post range distance surp origami robot nylon pvdf elastic polymers plastic hot plates reinforcement learning; multi-agent; mean-field; game theory; mean field; reinforcement learning current reinforcement learning; multi-agent; Xbee Zigbee robot compiler spi contact neural network dynamic modeling quasi-static modeling edg-examples Kalman Filter port-array von Mises Fisher von Mises-Fisher literature review multipack car Zero Elastic Energy modes swarm control solar cars system ID serial monitor edg-ide Discrete Elastic Rods ceres debug Consensus Algorithms coriolis force dynamic model proposal wtf deep learning pdms interpolation wireless signal strength reinforcement learning; multi-agent; decentralized misc reinforcement learning; multi-agent; mean-field; stationary demo video flytrap papers steering structured field pivoting differential power detectionrate color shape edg-refactoring pain python vision Machine Learning Q-Learning Model-Free release conferences quasi-static pushing liquid crystal elastomer nonholonomic systems iot grant feedback-controlled controls trajectory optimization surface contact Characterization tool ML multi-agent path finding Liquid Crystal Elastomers Learning kinematic_model reservoir computing 2.4 GHz concept 433 MHz Bayesian Network creative Computer skill internal silicone integrated system instance segmentation marginal cost pricing bootstrapping Bayesian networks ensemble methods offline Rl hardware manipulation COVID 19 paper cutter ESP32 kalman filter; multi-robot state space delta tolling buoyancy chiral square unit cell pressure distribution model prediction thrust configuration grid fabrication firmware protobuf #activecapturingmechanism #claw 3D-CHESS; kalman filter boxboat tracking model-based RL von Mises Distribution slam; flowchart; spring-mass 3D-CHESS; 433 rssi signal strength multirobot system writing in-situ design buoyancy equations boat deployment cell cameras der newton's method Barycenter Euler-Bernoulli beam sma-based actuator game theory Bessel functions von Mises-Fisher Distributions ide HDL board design battery current sensor ZMP center of friction Multi-Agent Systems code balloon semantic segmentation MIMO communications ICRA ICML guassian processes probabilistic neural networks graph generators MBRL batch learning ros edg-compiler multirobot optitrack adaptive control motor driver submission DNN kalman filtering point cloud 2.4ghz latency scenic codesign presentations machine training preliminary exam multiple devices inkscape material multi-object tracking ICLR Python actuation catching mechanism integration flapping color_segmentation lab_data result segmentation on multiple object and centers finding competition prelab multiple blimps pid defender Synthesizable Radio 3d printing kalman filter motor distribution barometer detection lift force depth estimation cad solidworks design tool pixracer pixhawk ardupilot flight controller regression fly test sensor selection