07 May

Tests on the modules of optimization problems

Tsang-Kai Chang slam

The optimization based SLAM formulate the optimization problem with two kinds of constraints. First, the pre-integrated IMU error establishes the constraints between two spatial states, or two poses. The other one is the reprojection error that links a spatial state and a landmark. In the optimization tool, we have to specify the Jacobian of the error, which tells the optimization tool which direction to make the entire cost smaller. While both the pre-integration model and the reprojection model are nonlinear, these two blocks are prone to error.

We develop the following two simple test schemes, modified from the okvis project, in order to make sure the these modules in our system is correct.

All the implementation can be found in my github repo.

Pre-integrated IMU error

In this test simulation, we generate the IMU data with 1kHz over a 0.1 sec duration, and we vary the noise density of the IMU measurements.

We first take the correct initial state and set it constant in the optimization problem. We then add some noise to the final state to see whether the optimization tool can successfully recover the correct final state based on the pre-integrated IMU data.

s0_fixed_rot_error s0_fixed_pos_error

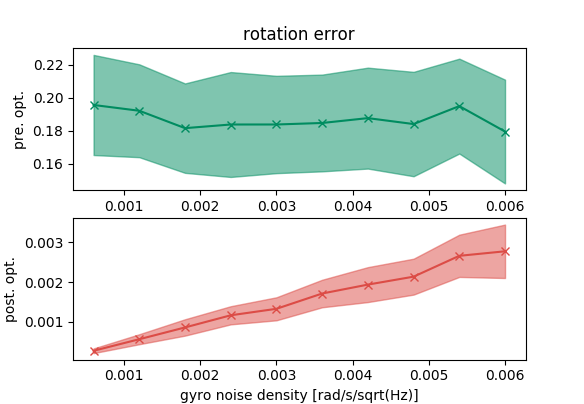
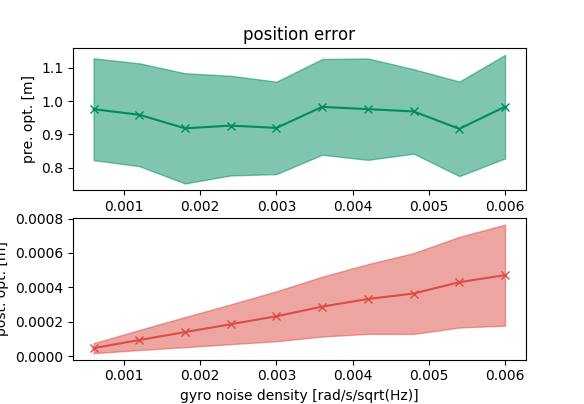
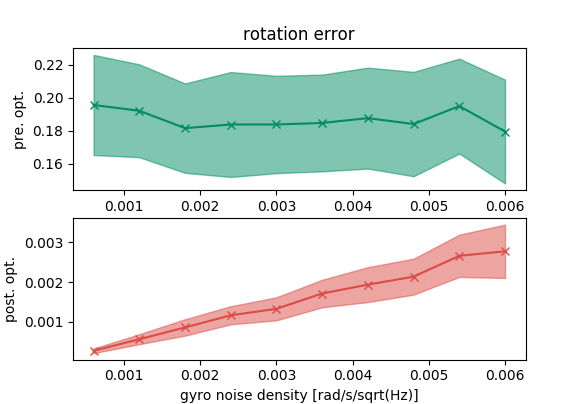
From the previous plots, we can see that the optimization tool can recover the final state. Furthermore, the errors of the recovered state grow with the IMU errors.

Now, we switch the role of the initial state and the final state. We use the correct final state in the optimization problem and set it constant to see if the optimization problem can find the correct initial state.

s1_fixed_rot_error s1_fixed_pos_error

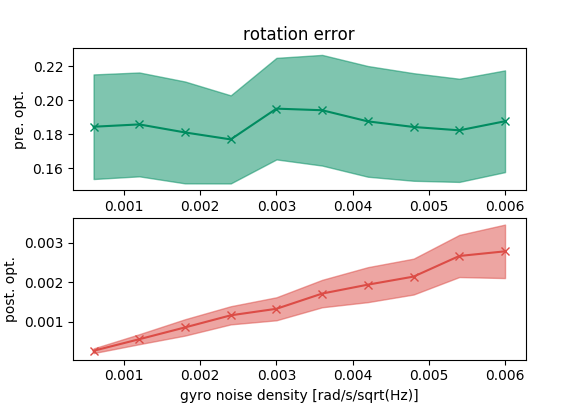
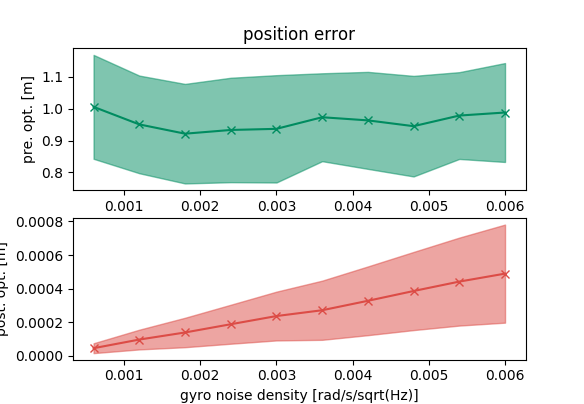
We observe the similar trend in this scenario that the optimization tool is correct.

Reprojection error

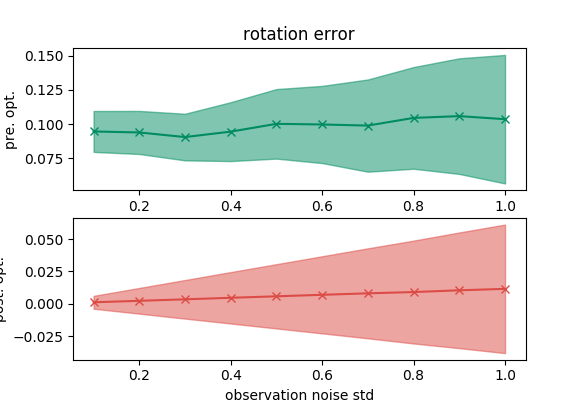
To test reprojection error, we randomly generate a pose, and then generate 100 random 3D points that the pose can observe. We then project those 100 points on the camera with that pose. In the optimization problem, we have 100 reprojection constraints. We set the correct landmarks in the optimization problem, and add random disturbance to the pose. The optimization tool is supposed to recover the pose.

We vary the observation noise and get the following plots, which show that the optimization tool does correctly to recover the pose.

reproj_rot_error reproj_pos_error

Next Post Previous Post

Search

Popular Tags

foray origami robots blimp ducky vr edg SLAM computer vision computational design roco slam Origami rocolib arduino RoCo design Robot Compiler simulation Motion Planning autonomy edg-model mesh reinforcement learning; multi-agent; mean-field; logics create; kalman filter; motors imu friction mesh network tank esp32 networking contacts multi-agent pushing auxetic machine learning dynamics esp now visual processing wireless control communication webapp pcbs structure ROCO i2c path planning cars Robotica reinforcement learning computer skill openmv test motor dataset visual DARPA odometry Battery surface structure power consumption dash port-arrays modeling origami paper frequency diversity semantic infrastructure auxetics feedback gondola machine vision Consensus bistable auxetic controller gestural intuition mixed reality unit cell robot crawler gestural interface open house network create; kalman filter; EM; refactoring 4-wheeled darpa; create; icra2021 apriltags lidar logic control FORAY perception Quantum Information crazyflie 433mhz optimization propeller Foray structures sensors environmental design radio DER Kullback-Leibler Divergence lasercutter tutorial von Mises Fisher Distribution IR simulink legs project management localization distributed optimization blynk Auxetics painlessmesh experiment results offline reinforcement learning exam research proposal altimeter thrust PCB sensor fusion gate or webots multi-agent path planning UAV RL integration test arnhold joystick balloon test vision processing pushing problem modeling contacts mesh networking motor configuration nodemcu swarm object detection fusionbot ros2 rviz2 gazebo conference matlab arduino nano decentralized surfaces keyboard IROS Integrated Demo throughput peripheral device paper review reinforcement learning; motorized boats Writing slam; paper review rhino Short Post range distance surp origami robot nylon pvdf elastic polymers plastic hot plates reinforcement learning; multi-agent; mean-field; game theory; mean field; reinforcement learning current reinforcement learning; multi-agent; Xbee Zigbee robot compiler spi contact neural network dynamic modeling quasi-static modeling edg-examples Kalman Filter port-array von Mises Fisher von Mises-Fisher literature review multipack car Zero Elastic Energy modes swarm control solar cars system ID serial monitor edg-ide Discrete Elastic Rods ceres debug Consensus Algorithms coriolis force dynamic model proposal wtf deep learning pdms interpolation wireless signal strength reinforcement learning; multi-agent; decentralized misc reinforcement learning; multi-agent; mean-field; stationary demo video flytrap papers steering structured field pivoting differential power detectionrate color shape edg-refactoring pain python vision Machine Learning Q-Learning Model-Free release conferences quasi-static pushing liquid crystal elastomer nonholonomic systems iot grant feedback-controlled controls trajectory optimization surface contact Characterization tool ML multi-agent path finding Liquid Crystal Elastomers Learning kinematic_model reservoir computing 2.4 GHz concept 433 MHz Bayesian Network creative Computer skill internal silicone integrated system instance segmentation marginal cost pricing bootstrapping Bayesian networks ensemble methods offline Rl hardware manipulation COVID 19 paper cutter ESP32 kalman filter; multi-robot state space delta tolling buoyancy chiral square unit cell pressure distribution model prediction thrust configuration grid fabrication firmware protobuf #activecapturingmechanism #claw 3D-CHESS; kalman filter boxboat tracking model-based RL von Mises Distribution slam; flowchart; spring-mass 3D-CHESS; 433 rssi signal strength multirobot system writing in-situ design buoyancy equations boat deployment cell cameras der newton's method Barycenter Euler-Bernoulli beam sma-based actuator game theory Bessel functions von Mises-Fisher Distributions ide HDL board design battery current sensor ZMP center of friction Multi-Agent Systems code balloon semantic segmentation MIMO communications ICRA ICML guassian processes probabilistic neural networks graph generators MBRL batch learning ros edg-compiler multirobot optitrack adaptive control motor driver submission DNN kalman filtering point cloud 2.4ghz latency scenic codesign presentations machine training preliminary exam multiple devices inkscape material multi-object tracking ICLR Python actuation catching mechanism integration flapping color_segmentation lab_data result segmentation on multiple object and centers finding competition prelab multiple blimps pid defender Synthesizable Radio 3d printing kalman filter motor distribution barometer detection lift force depth estimation cad solidworks design tool pixracer pixhawk ardupilot flight controller regression fly test sensor selection