For explicit-landmark optimization-based SLAM systems, the skeleton of SLAM backend can be considered as a nonlinear least-squares optimization problem, or \((\hat{s}_{1:n}, \hat{\lambda}) = {arg\,min}_{({s}_{1:n}, {\lambda})}\, \sum_{t=0}^{n-1} \| s_{t+1} - f(s_t, u_t) \|^2_{Q} + \sum_{t=1}^n \| o_t - h(s_t, \lambda) \|^2_{R}.\)
In the optimization problem, there are two constraints: the time propagation constraints from IMU sensors, and observation constraints from cameras.
I use ceres to implement this optimization problem. This post summarizes the backend debugging process.
Time propagation error
The initial values are determined by the ground truth data. I tested the dead reckoning from IMU data to begin with.
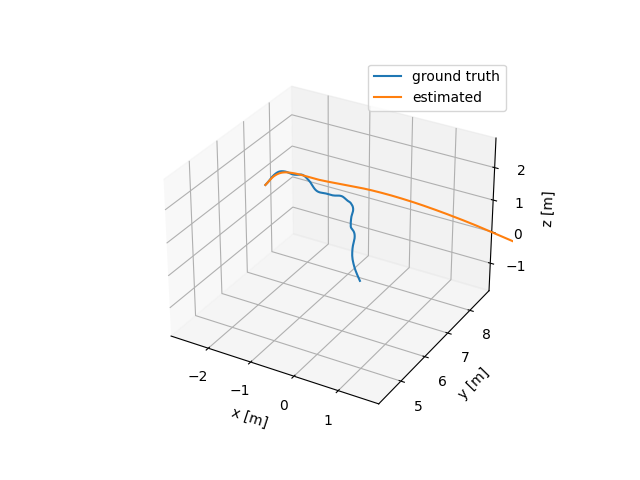
The estimated trajectory looks fine initially, but diverges as time goes by. Then I added IMU biases to see the effects.
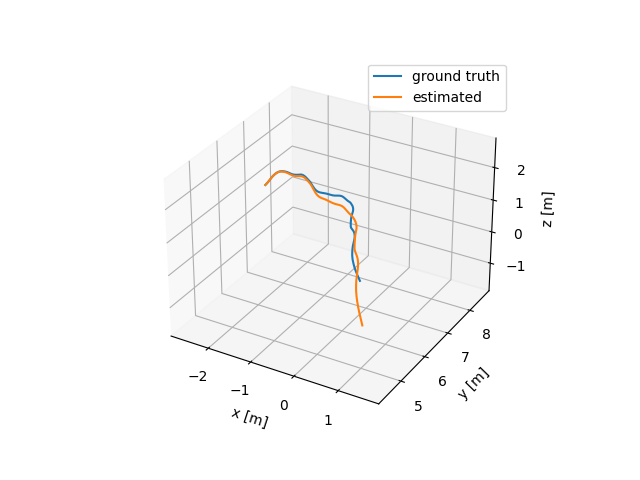
Basically, IMU biases are essential to describe the dynamics. Even though IMU biases are time varying, they can be considered constant within short amount of time. Currently, I used the bias data from the ground truth data, but the biases can be determined as parameters in the optimization problem. I think this is relatively straightforward.
Reprojection error
The first problem I face is that I am not sure the transformation in the configuration file is from the body frame to the camera frame, or the opposite. I tested both cases, and the results seem unsatisfactory.
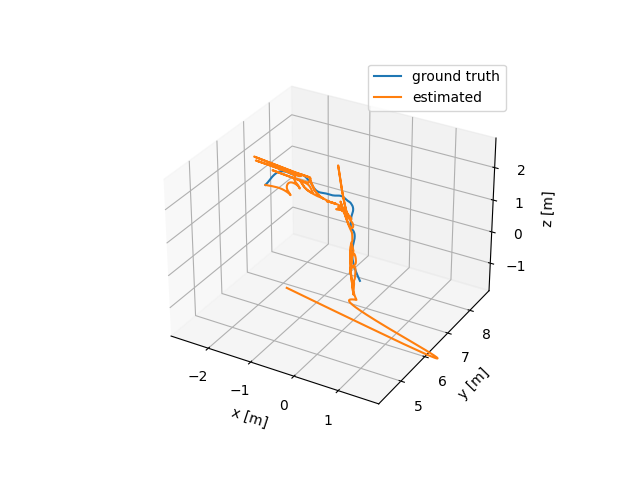
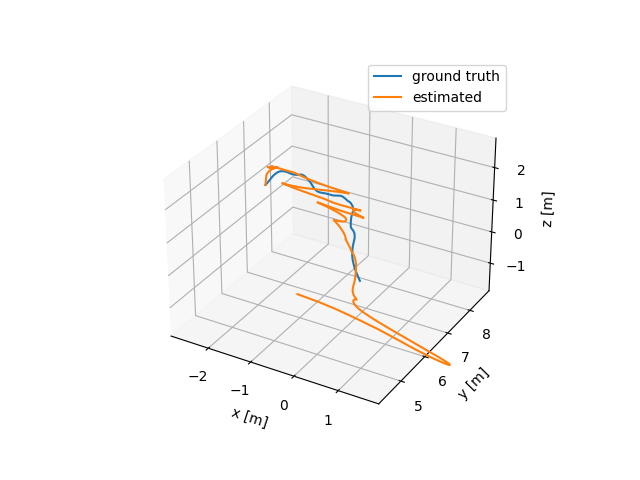
I think this might have to do with the initial values of landmarks, which are nowhere to be known. We may use triangularization to initialize the landmark positions.
Next steps (before EM-based approaches)
- incorporating covariance matrices in the optimization problem
- initializing landmark positions by triangularization
- implementing local parameterization, especially for the rotation representation
- implementing marginalization strategy, which enables optimization-based algorithms online