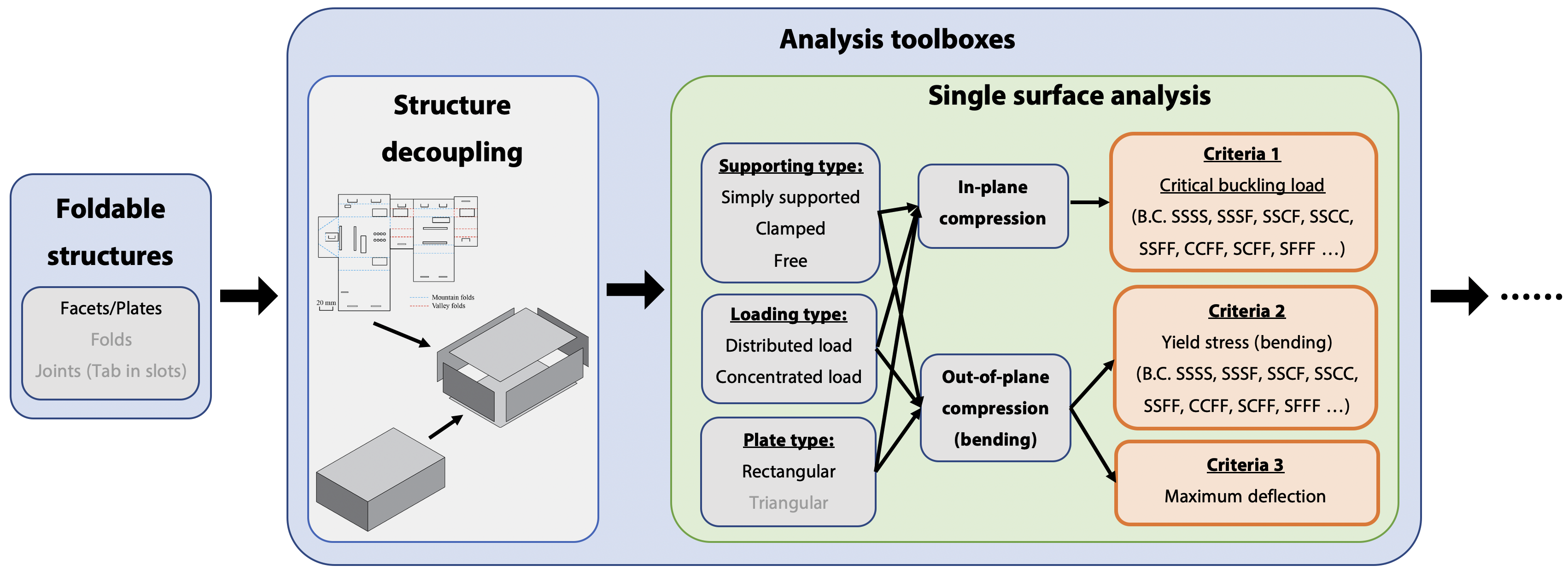
High-Level View: computational design of foldable structures

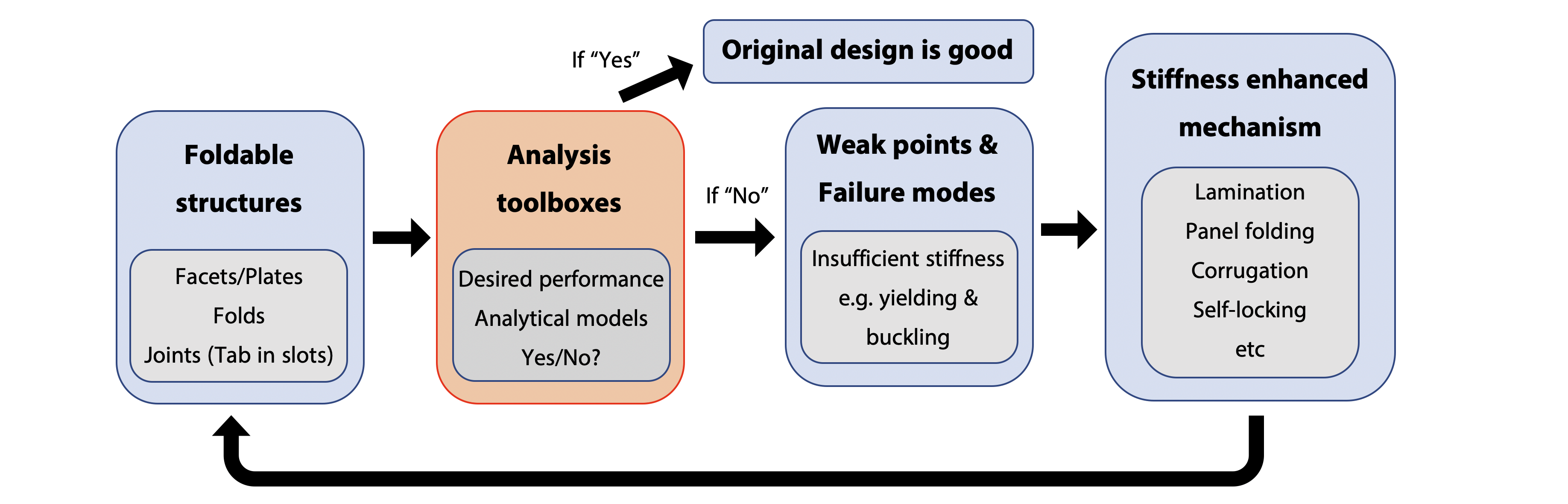
Updates

During the past week, I have been working on finidng numerical solutions for plate failures under different boundary conditions and loading conditions.

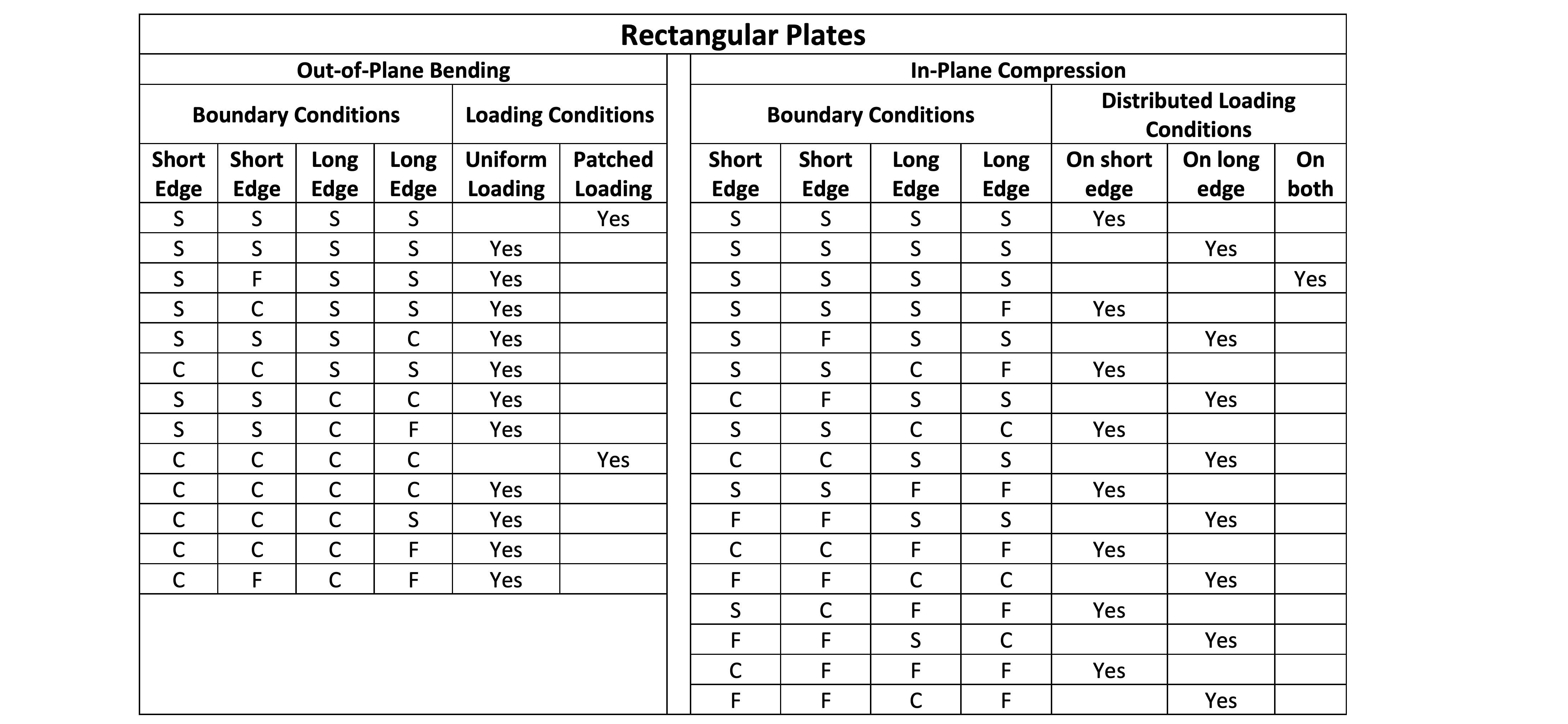
For a plate, there are three types of boundary conditions:

(1) simply supported

(2) clamped

(3) free

There are three types of forces that can be applied to a plate:

(1) In-plane compression/tension

(2) Out-of-plane bending

(3) Shearing

Note: Let's forcus on in-plane compression load and out-of-plane bending load for now, since these two are most commonly seen in foldable structures.

There are three types of failure (due to the above two types of load):

(1) Buckling: caused by in-plane compression load

(2) Bending yield: caused by out-of-plane load

(3) Overly deflect: caused by out-of-plane load

Assumptions for Numerical Solutions for Thin Plate:

(1) The plate is flat, of uniform thickness, and of homogeneous isotropic material;

(2) The thickness is not more than about one-quarter of the least transverse dimension, and the maximum deflection is not more than about one-half the thickness; (For larger deformation, it will be membrane problem, instead of plate problem)

(3) All forces—loads and reactions—are normal to the plane of the plate;

(4) The plate is nowhere stressed beyond the elastic limit.

(5) Poisson's ratio v ~= 0.3.

This week, I have done some research on calculating the critical buckling load and applied bending stress in a plate under the following load/boundary conditions. Those covers the most commonly seen situations. These will be used to determine the critical load in our design toolbox.

By far, we have done determining failure cirteria. Current input to the design toolbox are: individual plate with boundary conditions, loading conditions. Output will be critical load and failure 'boolean'.

During the coming week, I will work on decoupling foldable structure in order to study each plate individually.

Next Post Previous Post