08 Jan

Plate Buckling Study, Irregular-Shaped Plate

Chang Liu origami robots

I am currently studying this paper On Solving the Irregularly-Shaped Plate Buckling Problem.

  • "Traditional finite element theory assumes a set of displacement functions that are nodally based and minimizes the potential energy with respcct to the nodal coordinates."

  • "The method of this paper provides a general displacement function with unknown coefficients and without regard to the element’s nodes."

  • "The only drawback to the present method is that it is limited to relatively simple plates defined by eight nodes and simply connected plates (no holes)."

  • Background knowledge 1: Gaussian quadrature. "Gauss quadrature allows integration of functions by simply evaluating functions at certain points, called Gauss points, rather than actually integrating using a technique such as Simpson's Rule or Romberg integration."

  • Background knowledge 2: Lagrange multiplier

  • Background knowledge 3: Subparametric mapping

  • Background knowledge 4: Plane stress and plane strain

At the same time, I am researching other articles to solve what I don't understand in this paper.

  • "However, for many other boundary conditions, simple displacement functions like Equation (6.19) do not exist, and in some cases analytical, exact solutions analogous to Equations (6.21) and (6.31) have not been found. In those cases approximate solutions have been found using energy methods, which will be discussed in Chapters 8 and 9." See this article here: BUCKLING OF ISOTROPIC COLUMNS AND PLATES.pdf.

  • Rayleigh-Ritz method for analysis (minimum potential energy theorm):

Precedures, Method Write-up

-

Step 1: Subparametric Mapping in FEA System. (I have no background in this, so it took a while to get the information I needed and some time to learn this knowledge.)

  • Goal: This is for transforming irregular shaped plane into square shape in another coordinate system. This will make integration easier.

  • See details in my note here.

  • I studied 'subparametric mapping'. From Cartesian domian into (\(\zeta\), \(\eta\)) domain.

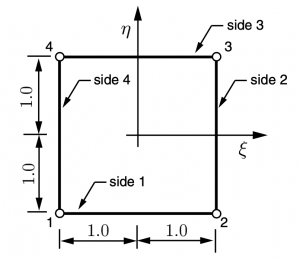
  • A figure of (\(\zeta\), \(\eta\)) domain, a quadrilateral element:

  • For a polygon, with number of edges no greater than 8, we can use 8-node mapping method to change coordinates from Cartesian domian into (\(\zeta\), \(\eta\)) domain. I did not get the same result as that presented in the paper. I assume it is because the node sequence I use is different than the one used in the paper, which is not clearly stated. But my result also make sense. I will use the result from this paper in my later calculation.

  • The reason for doing this mapping is for easy integration in later steps.

  • A good reference can be found here if you want to learn. Here is another one about quadrilateral element. Here is a useful website.

Step 2: Plane Stress, Strain Energy U Calculation.

  • See details in my note here.
Step 3: Plane Stress, Virtual Work Energy T Calculation.

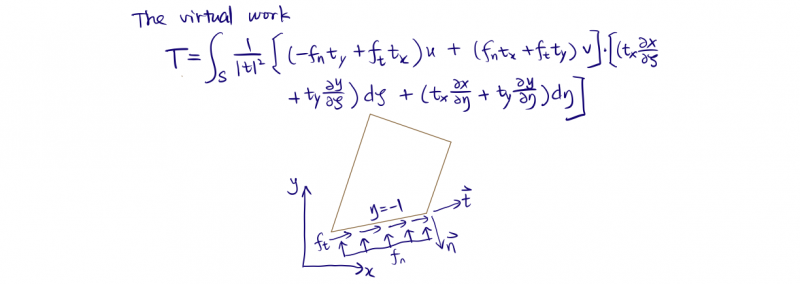
  • See details in my note here.
Step 4: Solving Coefficients Using Minimum Potential Energy Method.
  • Goal: get in-plane displacement \(u\) and \(v\), in order to get plane stress and strain. This plane stress and strain will be later applied to calculate bucalking virtual work energy. The reason to do it this way is because, for irregular shaped polygon, it is hard to calculate loading conditions on edges.

  • Detailed calculation steps / validations on Lagrange multiplier are shown below:

  • See details in my note here.
Step 5: Buckling (Bending), Strain Energy U Calculation.

  • A full derivative of \(\frac{\partial \zeta}{\partial x}\), \(\frac{\partial \zeta}{\partial y}\), \(\frac{\partial \eta}{\partial x}\) and \(\frac{\partial \eta}{\partial y}\) can be solved using a method called implicit derivative and using Mathemetica, results can be found here.

  • See details in my note here.

Step 6: Buckling (Bending), Virtual Work Energy T Calculation.

  • See details in my note here.
Step 7: Solving Coefficients Using Minimum Potential Energy Method.
  • Goal: calculate buckling load (coefficients).

  • See details in my note here.
A Concrete Detailed Calculation

Steps_Details.pdf

Summary:

  • {As of Jan 13, 2021} (Almost) All clear! Start working on implementation.

  • {As of Jan 11, 2021} There are not enough information in the paper that can lead me to solve the problem by writing down all necessary equations.

  • {As of Jan 11, 2021} The precedure seems to be limited to 8-nodes only.

  • {As of Jan 11, 2021} The bending problem seems to be limited to rectangular only (if I understand correctly). And the expression of external load \(N_x\), \(N_y\) and \(N_{xy}\) seems to indicating the loading is quite specialized.

  • {As of Jan 11, 2021} How to convert boundary conditions from one coordinate system to another is question to solve. In (\(\zeta\), \(\eta\)) domain, how to incorporate the BSc into the energy equation is still a question.

Past Weeks' Updates

Check here

Next Post Previous Post

Search

Popular Tags

foray origami robots blimp ducky vr edg SLAM computer vision computational design roco slam Origami rocolib arduino RoCo design Robot Compiler simulation Motion Planning autonomy edg-model mesh reinforcement learning; multi-agent; mean-field; logics create; kalman filter; motors imu friction mesh network tank esp32 networking contacts multi-agent pushing auxetic machine learning dynamics esp now visual processing wireless control communication webapp pcbs structure ROCO i2c path planning cars Robotica reinforcement learning computer skill openmv test motor dataset visual DARPA odometry Battery surface structure power consumption dash port-arrays modeling origami paper frequency diversity semantic infrastructure auxetics feedback gondola machine vision Consensus bistable auxetic controller gestural intuition mixed reality unit cell robot crawler gestural interface open house network create; kalman filter; EM; refactoring 4-wheeled darpa; create; icra2021 apriltags lidar logic control FORAY perception Quantum Information crazyflie 433mhz optimization propeller Foray structures sensors environmental design radio DER Kullback-Leibler Divergence lasercutter tutorial von Mises Fisher Distribution IR simulink legs project management localization distributed optimization blynk Auxetics painlessmesh experiment results offline reinforcement learning exam research proposal altimeter thrust PCB sensor fusion gate or webots multi-agent path planning UAV RL integration test arnhold joystick balloon test vision processing pushing problem modeling contacts mesh networking motor configuration nodemcu swarm object detection fusionbot ros2 rviz2 gazebo conference matlab arduino nano decentralized surfaces keyboard IROS Integrated Demo throughput peripheral device paper review reinforcement learning; motorized boats Writing slam; paper review rhino Short Post range distance surp origami robot nylon pvdf elastic polymers plastic hot plates reinforcement learning; multi-agent; mean-field; game theory; mean field; reinforcement learning current reinforcement learning; multi-agent; Xbee Zigbee robot compiler spi contact neural network dynamic modeling quasi-static modeling edg-examples Kalman Filter port-array von Mises Fisher von Mises-Fisher literature review multipack car Zero Elastic Energy modes swarm control solar cars system ID serial monitor edg-ide Discrete Elastic Rods ceres debug Consensus Algorithms coriolis force dynamic model proposal wtf deep learning pdms interpolation wireless signal strength reinforcement learning; multi-agent; decentralized misc reinforcement learning; multi-agent; mean-field; stationary demo video flytrap papers steering structured field pivoting differential power detectionrate color shape edg-refactoring pain python vision Machine Learning Q-Learning Model-Free release conferences quasi-static pushing liquid crystal elastomer nonholonomic systems iot grant feedback-controlled controls trajectory optimization surface contact Characterization tool ML multi-agent path finding Liquid Crystal Elastomers Learning kinematic_model reservoir computing 2.4 GHz concept 433 MHz Bayesian Network creative Computer skill internal silicone integrated system instance segmentation marginal cost pricing bootstrapping Bayesian networks ensemble methods offline Rl hardware manipulation COVID 19 paper cutter ESP32 kalman filter; multi-robot state space delta tolling buoyancy chiral square unit cell pressure distribution model prediction thrust configuration grid fabrication firmware protobuf #activecapturingmechanism #claw 3D-CHESS; kalman filter boxboat tracking model-based RL von Mises Distribution slam; flowchart; spring-mass 3D-CHESS; 433 rssi signal strength multirobot system writing in-situ design buoyancy equations boat deployment cell cameras der newton's method Barycenter Euler-Bernoulli beam sma-based actuator game theory Bessel functions von Mises-Fisher Distributions ide HDL board design battery current sensor ZMP center of friction Multi-Agent Systems code balloon semantic segmentation MIMO communications ICRA ICML guassian processes probabilistic neural networks graph generators MBRL batch learning ros edg-compiler multirobot optitrack adaptive control motor driver submission DNN kalman filtering point cloud 2.4ghz latency scenic codesign presentations machine training preliminary exam multiple devices inkscape material multi-object tracking ICLR Python actuation catching mechanism integration flapping color_segmentation lab_data result segmentation on multiple object and centers finding competition prelab multiple blimps pid defender Synthesizable Radio 3d printing kalman filter motor distribution barometer detection lift force depth estimation cad solidworks design tool pixracer pixhawk ardupilot flight controller regression fly test sensor selection