30 Dec

Plate bending, Method of Weighted Residual (MWR) & Plate Buckling

Chang Liu origami robots

Remarks

  • MWR for plate bending, code clean up. Code can be found here

  • Plate buckling research.

  • Try solving buckling equation using MWR. (Result: Not how it works. So I need to try something else.)

Details

Dec 28, 2020 (Monday)

  • MWR for plate bending, code clean up. Code can be found here

  • Plate buckling research. Looks like there is also a 4th order governing equation and some boundary conditions to be used to solve the buckling in plates.

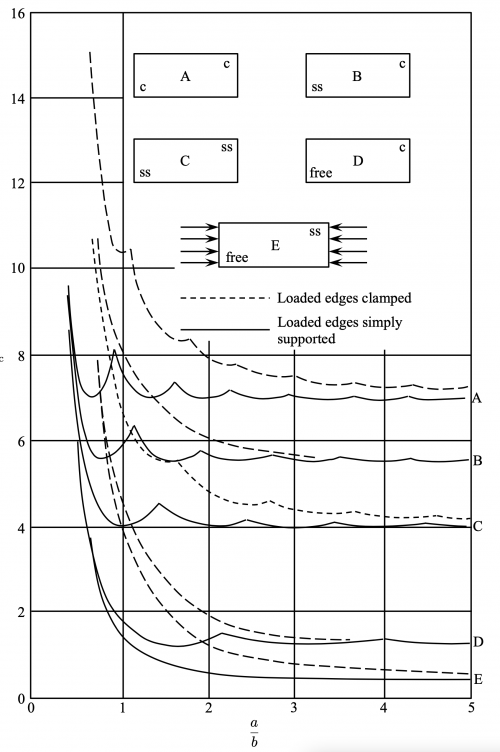
  • "The unloaded edges of rectangular plates can be either simply supported (ss), clamped (c) or free. The loaded edges could be either simply supported or clamped. This gives rise to ten different combination. The buckling coefficient is plotted against the plate aspect ratio a/b." [1]

[1]

  • Plate buckling explanation:

Useful video 1

Useful video 1 This one is really good!

Dec 29, 2020 (Tuesday)

(a) Straight lines perpendicular to the mid-surface (i.e., transverse normals) before deformation remain straight after deformation.

(b) The transverse normals do not experience elongation (i.e., they are inextensible).

(c) The transverse normals rotate such that they remain perpendicular to the mid-surface after deformation." [2]

  • The governing equation for plate buckling is

\(\frac{\partial^4 \omega_{(x, y)}}{\partial x^4} + 2 \frac{\partial^4 \omega_{(x, y)}}{\partial x^2 \partial y^2} + \frac{\partial^4 \omega_{(x, y)}}{\partial y^4} + N_{xx} \frac{\partial^2 \omega_{(x, y)}}{\partial x^2} + N_{yy} \frac{\partial^2 \omega_{(x, y)}}{\partial y^2} = 0\)

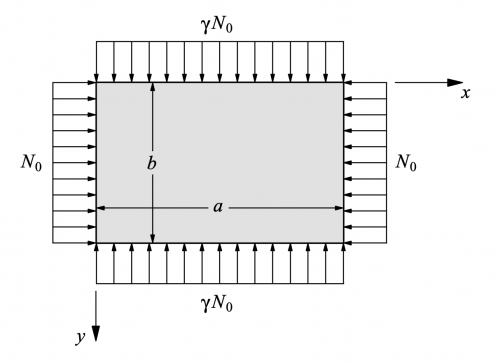
  • The boundary conditions are the same as plate bending:
  1. For a clamped, tilted edge, the boundary conditions are:

(1.a) \(\omega = 0\): deformation along edge is zero

(1.b) \(\frac{\partial \omega}{\partial n} = 0\): slope along normal direction is zero

  1. For a simply-supported, tilted edge, the boundary conditions are:

(2.a) \(\omega = 0\): deformation along edge is zero

(2.b) \(M_n = - D (\frac{\partial ^2 \omega}{\partial n ^2} + \nu \frac{\partial ^2 \omega}{\partial t ^2}) = 0\): moment along normal direction is zero

  1. For a free, tilted edge, the boundary conditions are:

(3.a) \(M_n = - D (\frac{\partial ^2 \omega}{\partial n ^2} + \nu \frac{\partial ^2 \omega}{\partial t ^2}) = 0\): moment along the tilted edge is zero

(3.b) \(R_n = - D (\frac{\partial ^3 \omega}{\partial n ^3} + (2 - \nu) \frac{\partial ^3 \omega}{\partial n \partial t ^2}) = 0\): reaction load along the tilted edge is zero

where \(n\) is the direction perpendicular to the tilted edge, \(t\) is the direction along the tilted edge.

  • Like plate bending, we now have a 4th order governing equation and some boundary conditions. Looks like we can use MWR to get approximate solutions for this plate buckling.

  • Some easy to notice / haven't been figured out questions:

  1. Is this governing equation suitable for other shapes (arbitrary shapes)?

  2. How to achieve the critical buckling load? (based on the definition, critical buckling load is the minimum buckling load, so shall we just find the minimum when we have approximated solutions?)

Dec 30, 2020 (Wednesday)

  • Keep doing research on plate buckling.

  • There are numerical / analytical solutions for some cases, these are for long rectanglar plates, (first and third BCs are on loading edge (width)):

SS-F-SS-F

C-F-C-F

SS-F-C-F

C-F-F-F

SS-SS-SS-SS

C-SS-SS-SS

C-SS-C-SS

SS-SS-F-SS

C-SS-F-SS

  • For short rectangular plate, which I believe we need to throughly study since I did see a lot of this type of plates in foldable structures, full analytical solution can be found in Timoshenko and Gere (1961). I will study this more tomorrow.

  • Notes for today's work can be found here.

Dec 31, 2020 (Thursday)
Jan 1, 2021 (Friday)
  • Happy New Year!!

To-Do List

  • Comparison of two plates.

  • The current implement works for convex polygons, and concave polygons with concaves vertically, but not horizontally. For a simple example:

  • ANSYS installation useful links:

https://uasatucla.org/docs/mechanical/tutorials/ansys_setup

https://www.seasnet.ucla.edu/ansys/

Next Post Previous Post

Search

Popular Tags

foray origami robots blimp ducky vr edg SLAM computer vision computational design roco slam Origami rocolib arduino RoCo design Robot Compiler simulation Motion Planning autonomy edg-model mesh reinforcement learning; multi-agent; mean-field; logics create; kalman filter; motors imu friction mesh network tank esp32 networking contacts multi-agent pushing auxetic machine learning dynamics esp now visual processing wireless control communication webapp pcbs structure ROCO i2c path planning cars Robotica reinforcement learning computer skill openmv test motor dataset visual DARPA odometry Battery surface structure power consumption dash port-arrays modeling origami paper frequency diversity semantic infrastructure auxetics feedback gondola machine vision Consensus bistable auxetic controller gestural intuition mixed reality unit cell robot crawler gestural interface open house network create; kalman filter; EM; refactoring 4-wheeled darpa; create; icra2021 apriltags lidar logic control FORAY perception Quantum Information crazyflie 433mhz optimization propeller Foray structures sensors environmental design radio DER Kullback-Leibler Divergence lasercutter tutorial von Mises Fisher Distribution IR simulink legs project management localization distributed optimization blynk Auxetics painlessmesh experiment results offline reinforcement learning exam research proposal altimeter thrust PCB sensor fusion gate or webots multi-agent path planning UAV RL integration test arnhold joystick balloon test vision processing pushing problem modeling contacts mesh networking motor configuration nodemcu swarm object detection fusionbot ros2 rviz2 gazebo conference matlab arduino nano decentralized surfaces keyboard IROS Integrated Demo throughput peripheral device paper review reinforcement learning; motorized boats Writing slam; paper review rhino Short Post range distance surp origami robot nylon pvdf elastic polymers plastic hot plates reinforcement learning; multi-agent; mean-field; game theory; mean field; reinforcement learning current reinforcement learning; multi-agent; Xbee Zigbee robot compiler spi contact neural network dynamic modeling quasi-static modeling edg-examples Kalman Filter port-array von Mises Fisher von Mises-Fisher literature review multipack car Zero Elastic Energy modes swarm control solar cars system ID serial monitor edg-ide Discrete Elastic Rods ceres debug Consensus Algorithms coriolis force dynamic model proposal wtf deep learning pdms interpolation wireless signal strength reinforcement learning; multi-agent; decentralized misc reinforcement learning; multi-agent; mean-field; stationary demo video flytrap papers steering structured field pivoting differential power detectionrate color shape edg-refactoring pain python vision Machine Learning Q-Learning Model-Free release conferences quasi-static pushing liquid crystal elastomer nonholonomic systems iot grant feedback-controlled controls trajectory optimization surface contact Characterization tool ML multi-agent path finding Liquid Crystal Elastomers Learning kinematic_model reservoir computing 2.4 GHz concept 433 MHz Bayesian Network creative Computer skill internal silicone integrated system instance segmentation marginal cost pricing bootstrapping Bayesian networks ensemble methods offline Rl hardware manipulation COVID 19 paper cutter ESP32 kalman filter; multi-robot state space delta tolling buoyancy chiral square unit cell pressure distribution model prediction thrust configuration grid fabrication firmware protobuf #activecapturingmechanism #claw 3D-CHESS; kalman filter boxboat tracking model-based RL von Mises Distribution slam; flowchart; spring-mass 3D-CHESS; 433 rssi signal strength multirobot system writing in-situ design buoyancy equations boat deployment cell cameras der newton's method Barycenter Euler-Bernoulli beam sma-based actuator game theory Bessel functions von Mises-Fisher Distributions ide HDL board design battery current sensor ZMP center of friction Multi-Agent Systems code balloon semantic segmentation MIMO communications ICRA ICML guassian processes probabilistic neural networks graph generators MBRL batch learning ros edg-compiler multirobot optitrack adaptive control motor driver submission DNN kalman filtering point cloud 2.4ghz latency scenic codesign presentations machine training preliminary exam multiple devices inkscape material multi-object tracking ICLR Python actuation catching mechanism integration flapping color_segmentation lab_data result segmentation on multiple object and centers finding competition prelab multiple blimps pid defender Synthesizable Radio 3d printing kalman filter motor distribution barometer detection lift force depth estimation cad solidworks design tool pixracer pixhawk ardupilot flight controller regression fly test sensor selection