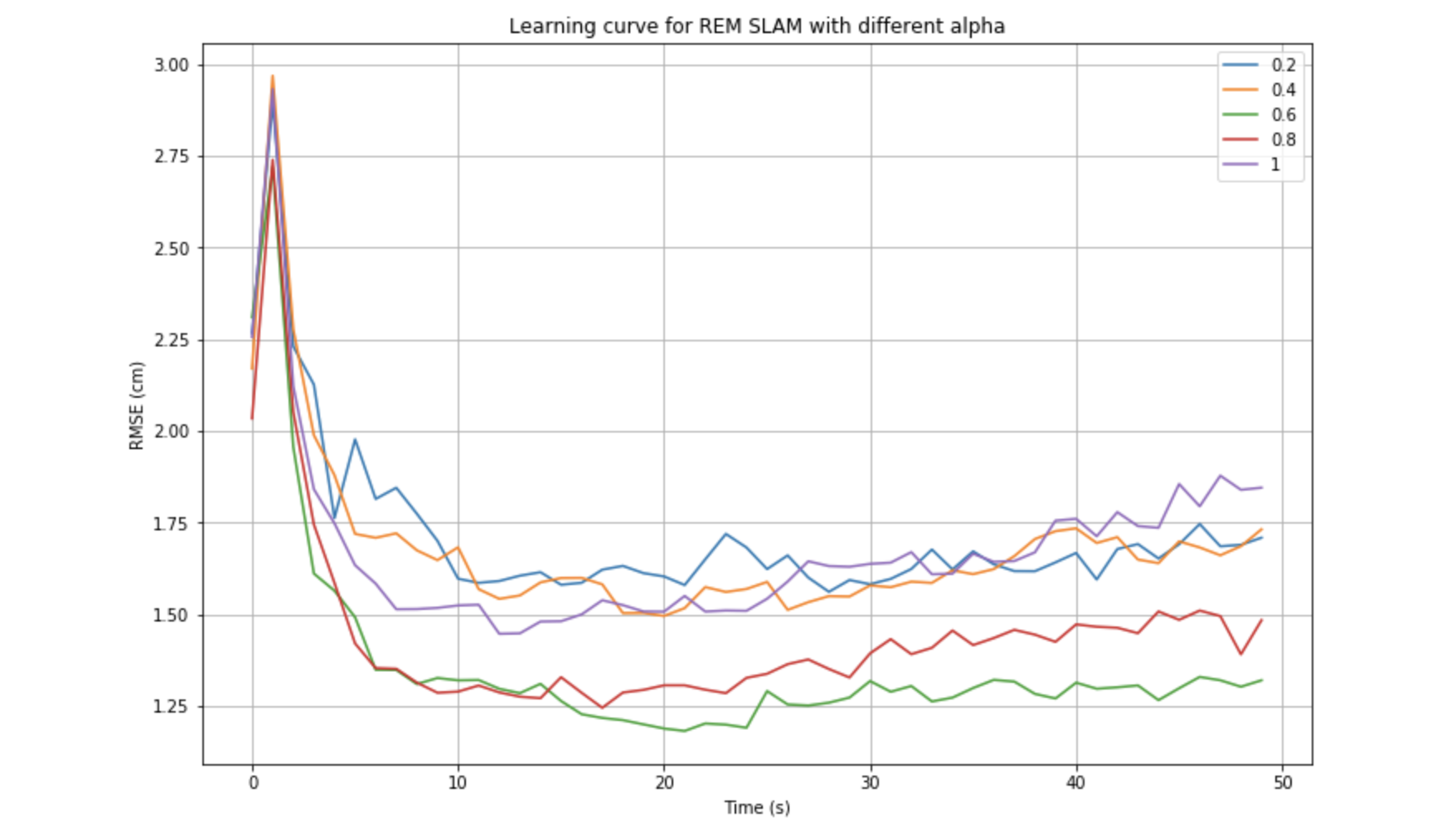
This week I've been revisiting the online EM for Hidden Markov Model [1]. The formulation between HMM and latent model is similar but there's a little different. I've also developed an performance evaluator to quantify and optimize the performance of our framework, especially the choice of learning rate gamma. Different choice of gamma has significant impact on performance. In online EM for latent data model [2], the choice of gamma is n^{-1}, where n is the iteration. While in this paper, the author proposed, empirically for HMM, the choice of gamma is n^{-0.6} to n^{-0.8}, and n^{-1} should never be chosen, but they didn't provide any proofs. This result is validated on our side.
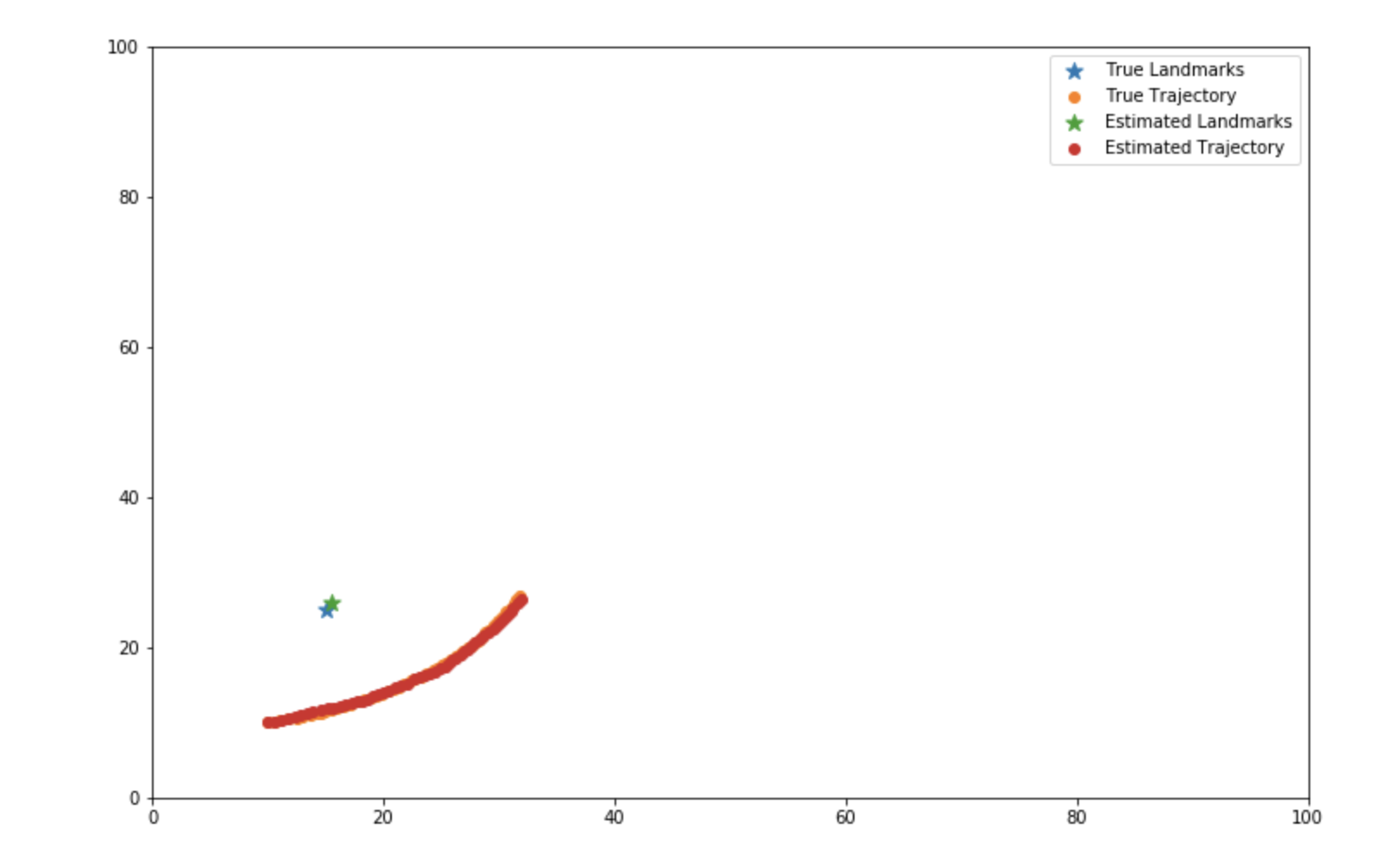
The settings of demo:
- Run Time: 5 seconds
- Input: [5.5 cm, 0.2 rad] per second
- Agent's prior: [10 cm, 10 cm, 0.2 rad]
- Landmark Position: [15, 25] cm
- Process noise:[1 cm^2, 0.0025 rad^2] per second
- Observation noise:[1 cm^2, 0.01 rad^2]
[1] Cappé, Olivier. "Online EM algorithm for hidden Markov models." Journal of Computational and Graphical Statistics 20.3 (2011): 728-749.
[2] Cappé, Olivier, and Eric Moulines. "On‐line expectation–maximization algorithm for latent data models." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 71.3 (2009): 593-613.