This week, we came up with some implementation idea that will fundamentally change Roco.
1 An inspiration that hit me while I was implementing face-edge connection
As I implement face-edge connection, I came to realize that to build a connection(let's say addConnection(B,A)), we really only need 6 pieces of information:
- face B
- face A
- the line segment(or the two endpoint of this line segment) where A and B intersects on FaceB
- the line segment(or the two endpoint of this line segment) where A and B intersects on FaceA
- the angle between A and B
- the orientation of A and B (front to front or front to back)
Edge-Edge uses these 6 pieces of information in a way that (3) and (4) are the edges of FaceB or FaceA.
Edge-Face uses these 6 pieces of information similar to edge-edge does. The only difference is that (3) is an edge of FaceB, but (4) is a line segment within FaceA.
Face-Face also uses these 6 pieces of information similarly to edge-face does. The only difference is that (3) is an edge of FaceB, but (4) is a line segment not within FaceA.
With this inspiration, I highly question if origarmi, or the data structure(we can roughly perceive this data structure as a dictionary) that implements the idea of origami, is appropriate or necessary for implementing furniture design. On the other hand, a tree really seems like a promising candidate.
2 How I envision the tree to work && Tree vs Origami
2.1 Tree vs Origami
Consider we are building this simple shape:
What origami forces us to do is that it only accept tree of two levels:
A
/ \
B C
(For each child-parent pair, let's call the parent inserting face, the child inserted face. I use passive and active sense to differentiate them.)
Why? In an abstract way of thinking, when B connects to A, origami deprives the ability of B to act as an inserting face. So C can only connect to the only inserting face left, which is A.
But if we discard the idea of origami, we actually gain more freedom without introducing any tricky potential issues (at least for the cases I can think of for now).
So, as long as the inserted face stores those six pieces of information for each of the face inserting on it respectively, we can build the structure more flexibly.
A tree that is allowed when origami is disregarded:
A
|
B
|
C
Notice child always in some sense, inherit the 3D placement of its parent. So C is B rotating 30 degrees from B itself (B is A rotating 30 degrees from the horizontal).
For now, I think as long as we first, build the tree; then, DFS the tree from the root, we are guaranteed to acquire a correct structure.
2.2 Why I think we need to "first, build the tree; then, DFS the tree from the root"? (This is a tentative idea).
Consider the user tries to build this, but the user build it by first connect A with B, then connect C with D, then connect B with C.
A correct tree structure should be:
A
|
B
|
C
|
D
We really needs to build the tree first and then DFS from the root, so that the algorithm will not falsely start from a internal C.
If the algorithm falsely starts from C, it may regard C as in the horizontal, D is 30 degrees from the horizontal. But when it connects B with C later, it thinks B as in the horizontal, and it must relocate C and all C's children to maintain the correct structure. When it connects A with B later, same thing needs to happen again.
So, we'd better build the tree first and DFS starting from the root. But I am not very sure about it at this point.
2.3 Another tree example: bookshelfWithBoard
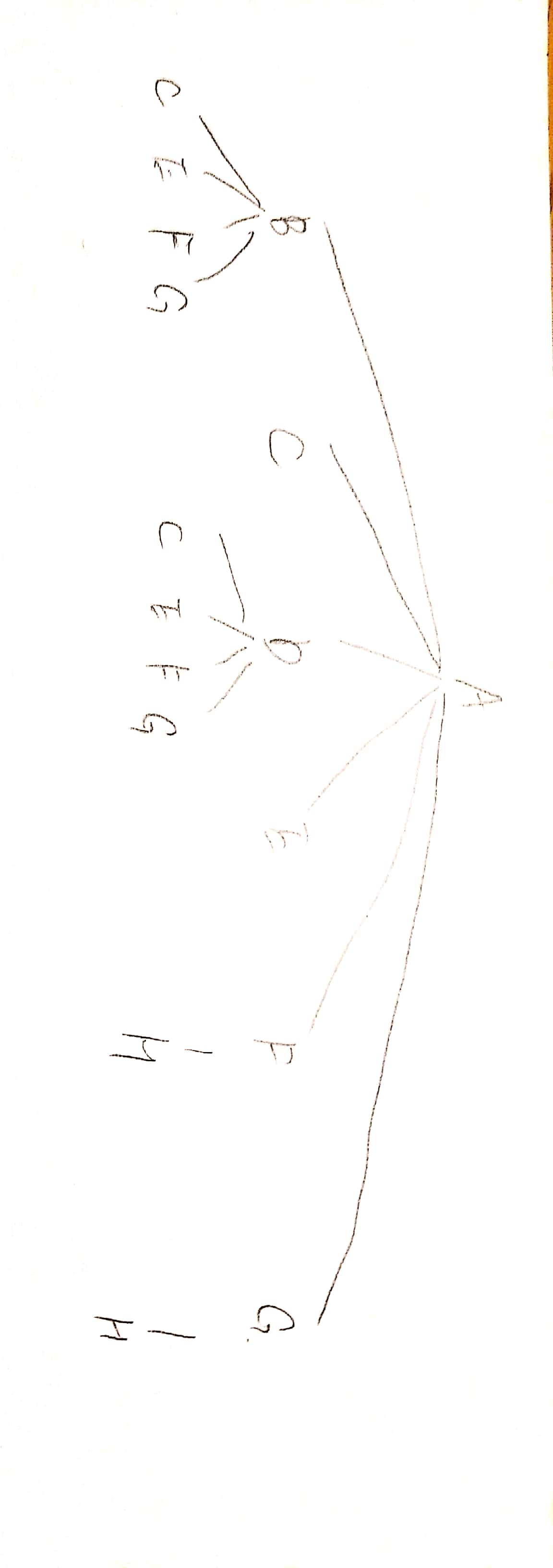
First, notice that the number of edges in the tree=The number of connections we need to add
Also, notice that a node can appear more than once in the tree. However, we can locate it at its first appearance in DFS, so its occurence afterwards are sort of redundant. This inspires Wenzhong and I to implement the validation mechanism. When we encounter this node again, we can check if the placement after this connection agrees with its current placement.