We have already proposed a multirobot localization algorithm that separates communication and observation as two independent mechanisms as well as keeps the estimation consistency. However, while localization is not the main goal but the support of more high-level tasks in most of the robotic systems, the scheduling problem of localization becomes our next focus. In other words, how can we use the least resource to fulfill certain localization performance requirement?
The corresponding continuous-time Riccati equation (CARE)
Even though the proposed algorithm can be easily analyzed in discrete-time Riccati recursion, the observation and communication rates are not explicit shown in the equation. Therefore, we find the limiting case of the original discrete-time Riccati recursion. The approach was extensively discussed the time when Kalman filtering was just proposed. Please refer to this paper.
The properties of the CARE
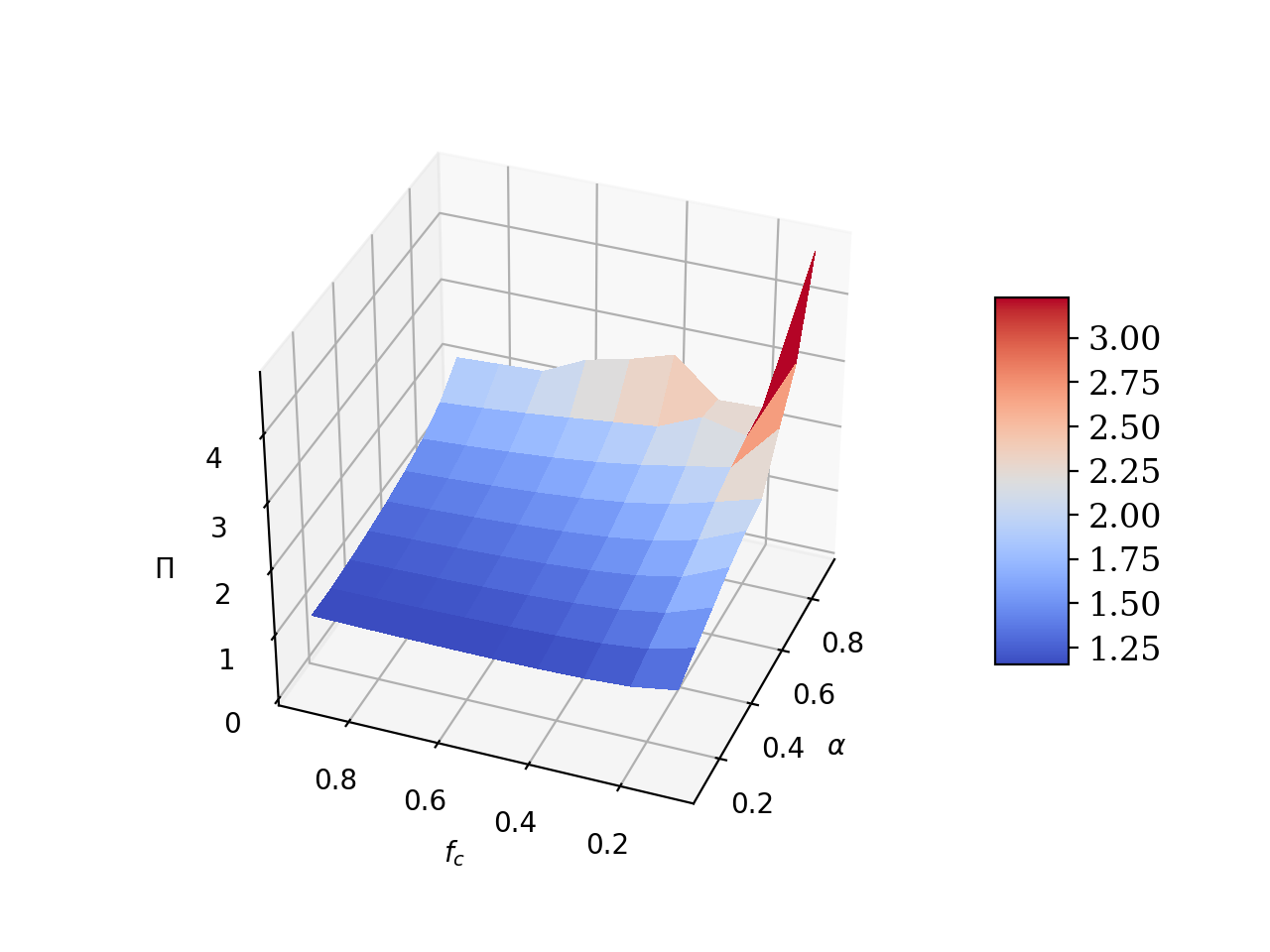
By applying the aforementioned method, we can get an implicit equation of the stationary estimation covariance and the operation rates. The next problem is that what is the effect of changing one of the parameter. In this paper, it shows that increasing observation rate just decreases the stationary covariance. However, our case is even more complicated. The following figure shows that there is no convexity property in some cases.
Tools from applied functional analysis
We use a very fancy tool called Fréchet derivative in functional analysis to deal with the CARE. While the mathematical definition may seem unfriendly at first (not really), the basic concept is quite straightforward: what is the derivative of a matrix?
For the detailed discussion, please wait for our publication.