Linearization of plate theory (4th order) for polygons (any amount of edges), with random tranverse loading
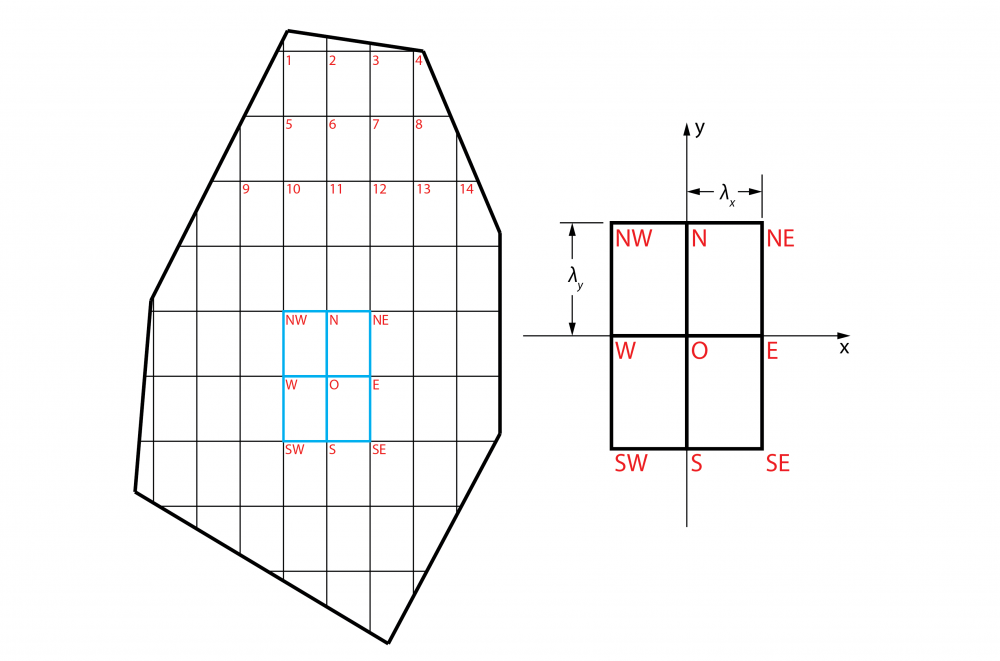
Given a random polygon, I first devide it into rectangulars. Then I label points at intersections.
Each unit is made out of four rectangulars, centered at each point.
Each unit will give me one linear difference equation (derived in notes at the end of this post). Therefore, I have N variables and N linear equations. Solving the linear equations will give us the deflection at each point. Using the deflections at points in each unit, I can calculate the moment, shear, reaction load at each node, as linear functions of the deflections of neighboring points.
Examples
Example #1
Number of edges: 3
Number of points: 479
Loading type: uniform loading across the plates
Edge boundary condition: simply supported
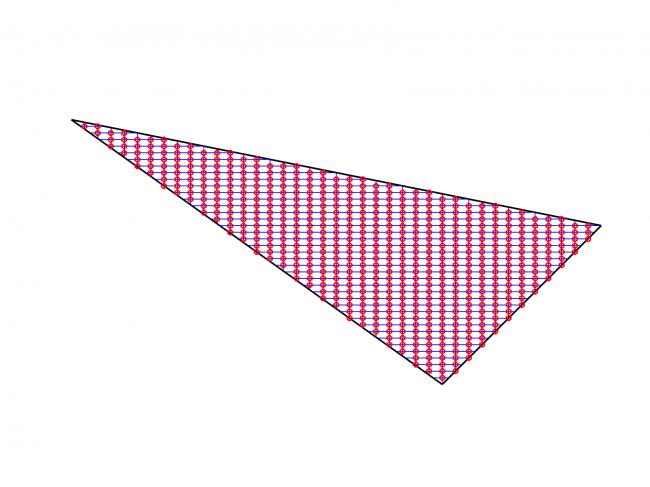
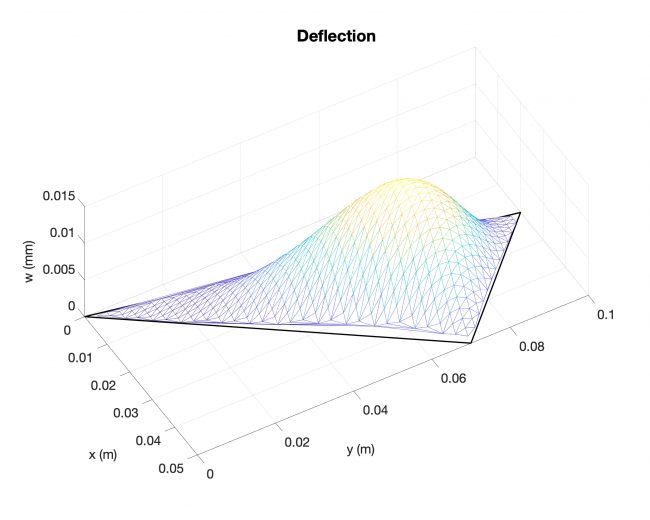
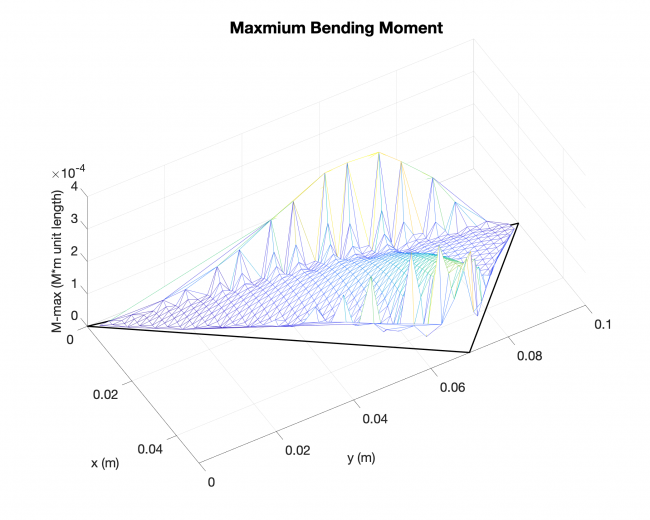
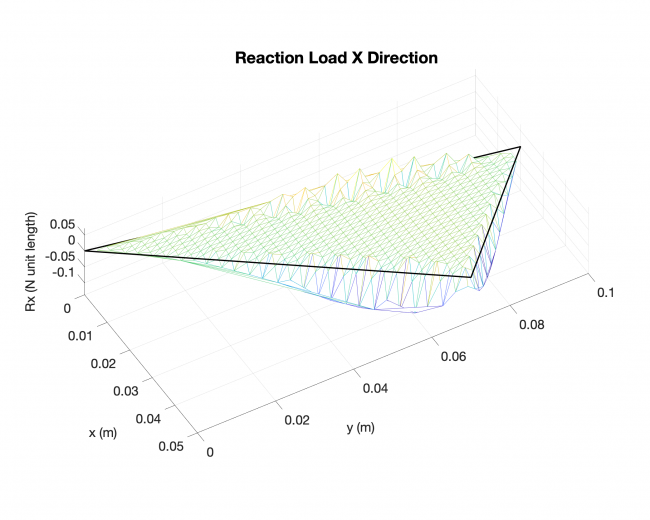
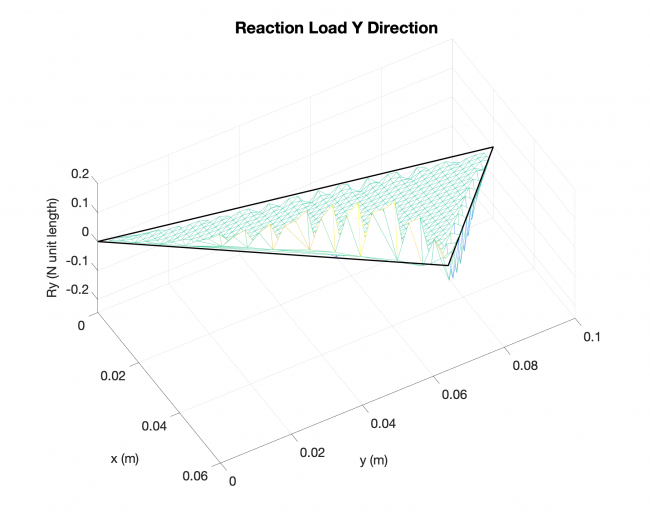
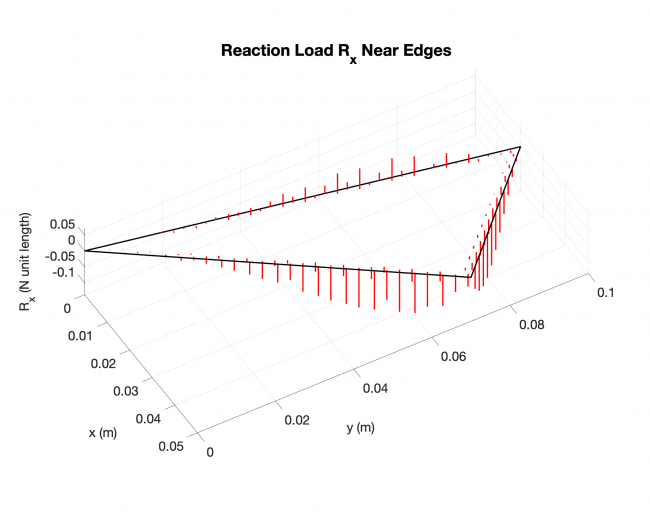
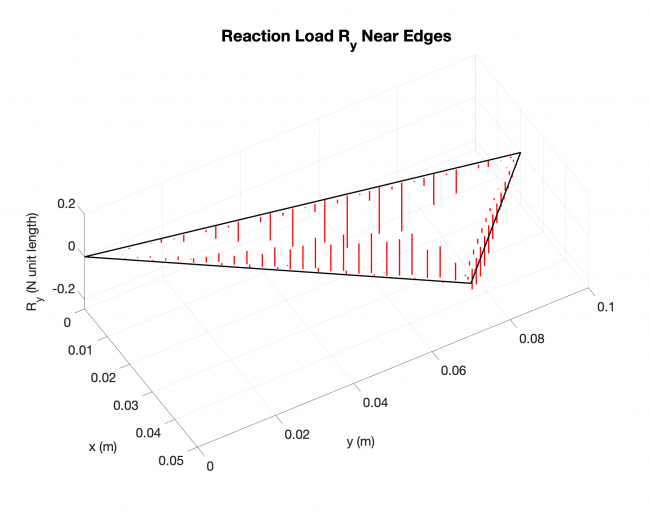
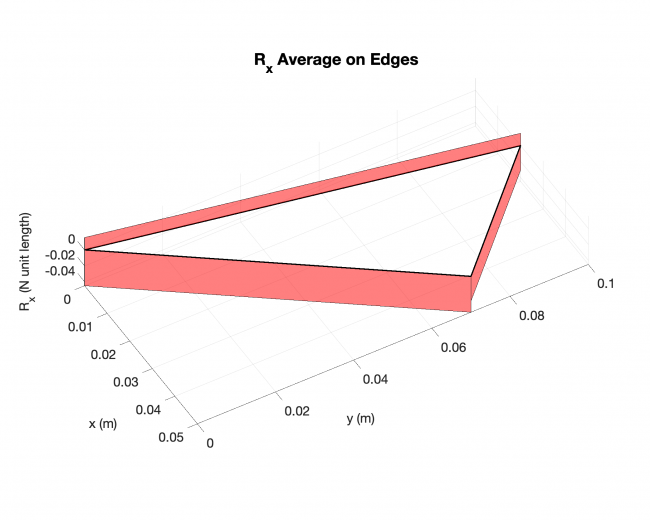
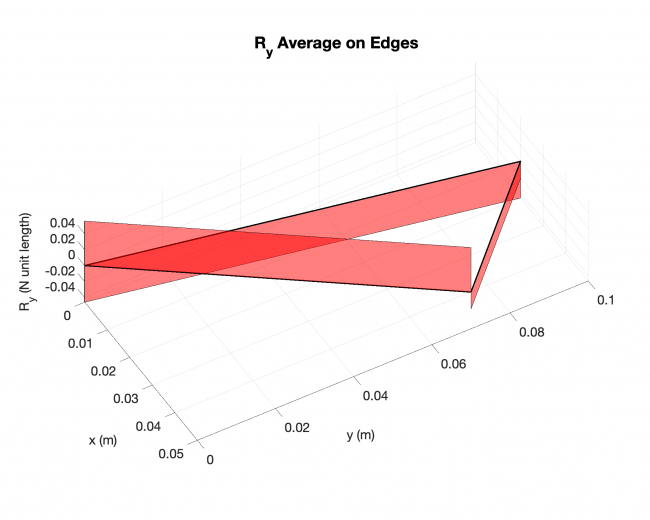
Example #2
Number of edges: 4
Number of points: 1521
Loading type: uniform loading across the plates
Edge boundary condition: simply supported

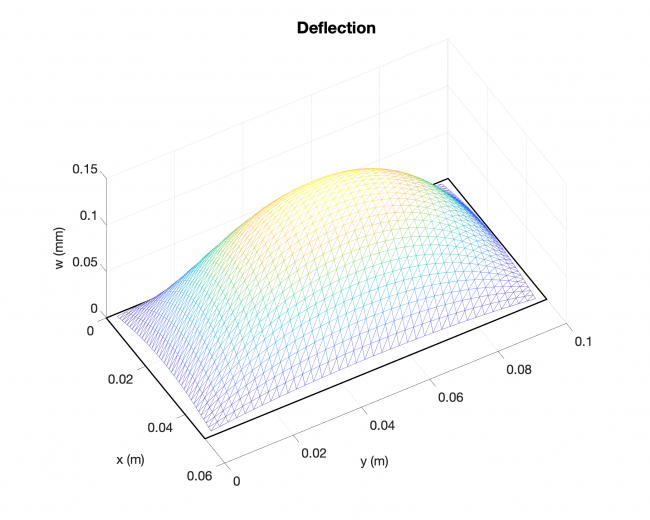
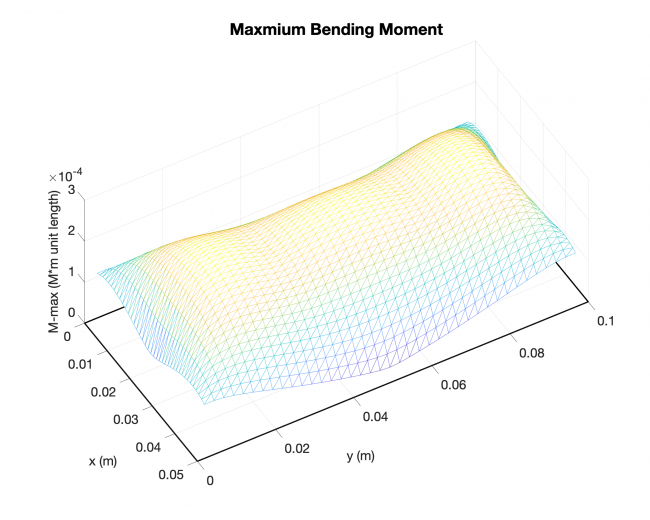
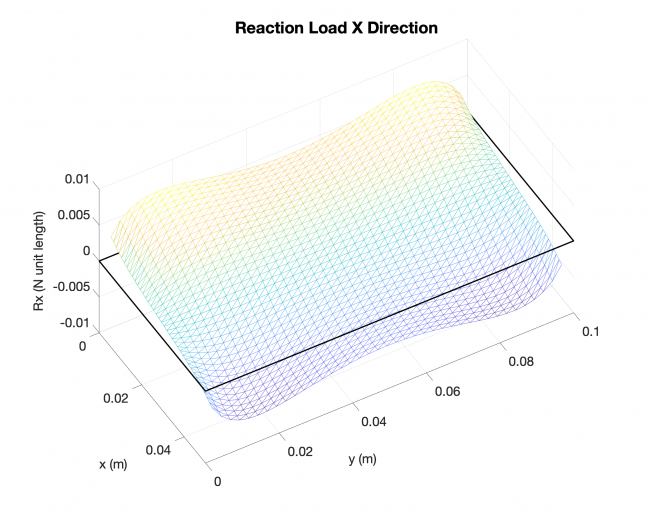
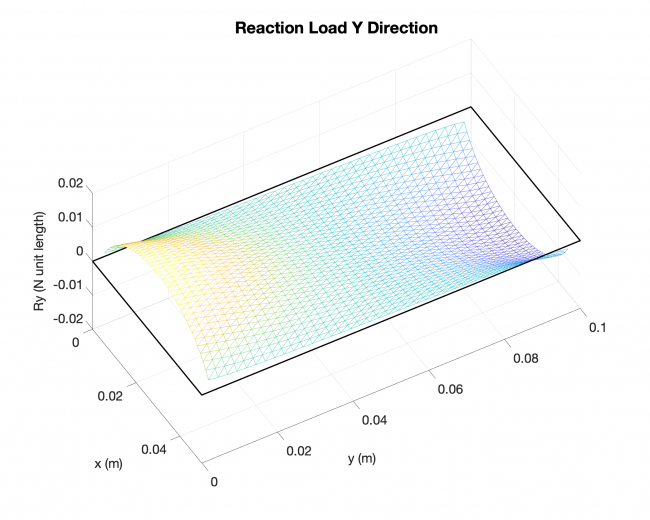
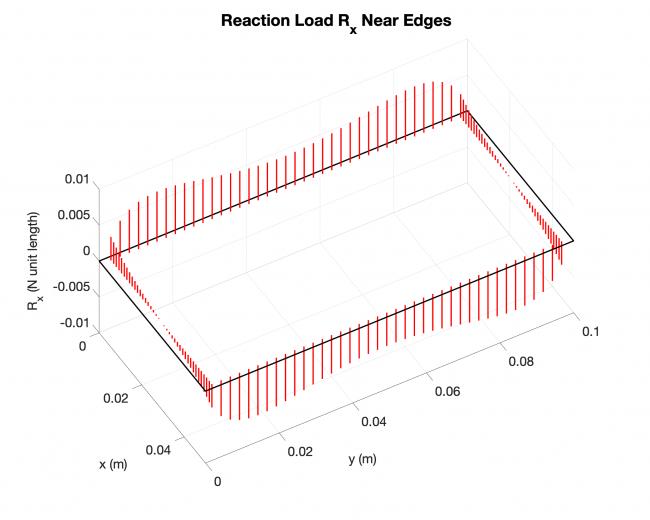
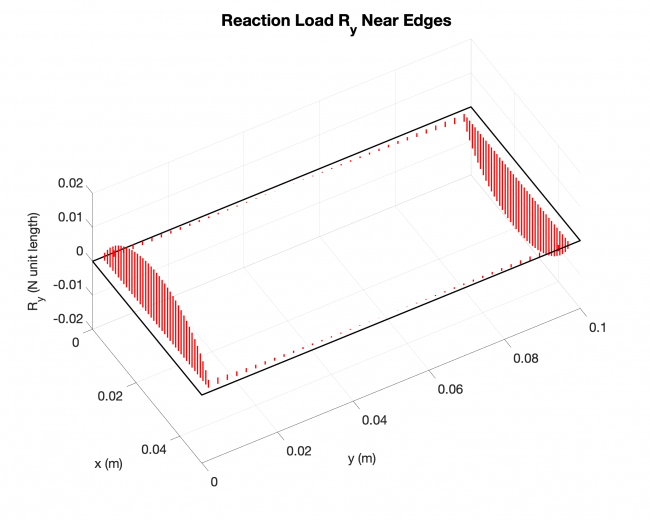
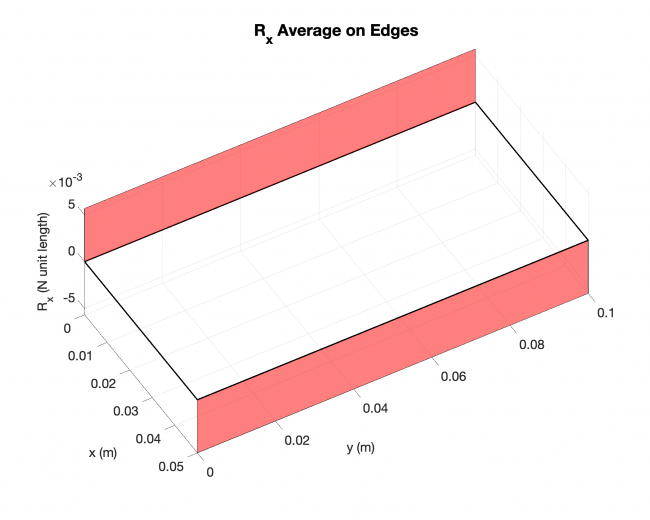
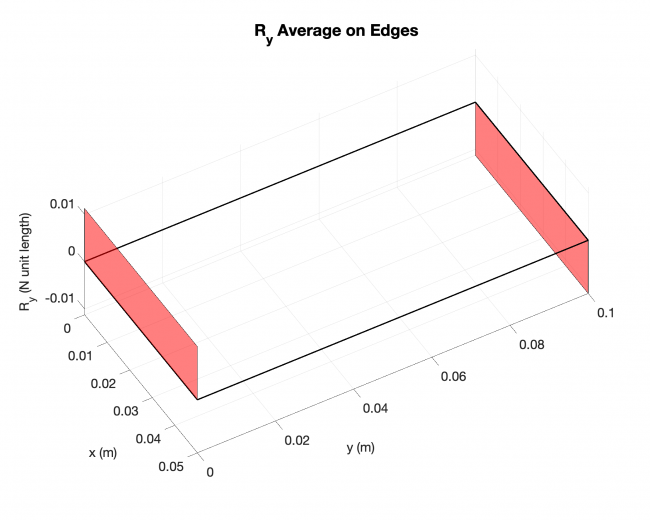
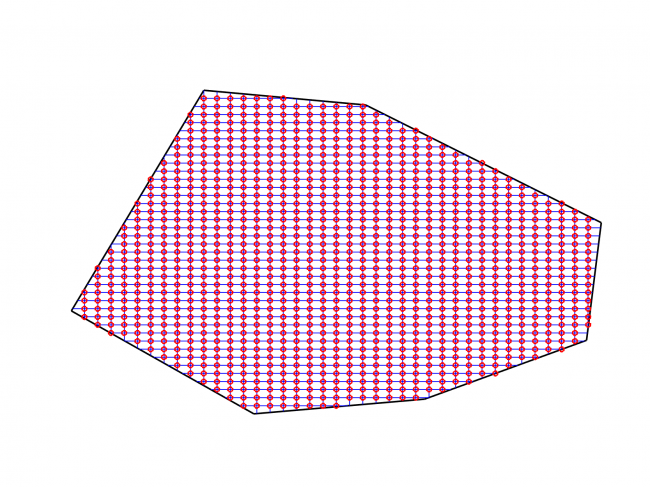
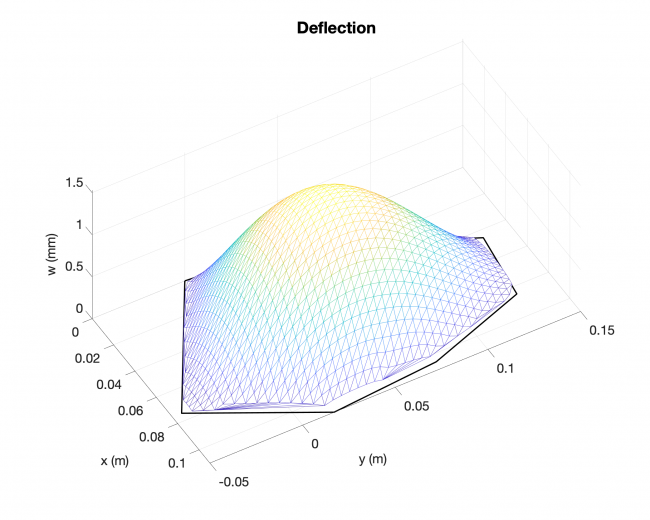
Example #3
Number of edges: 7
Number of points: 1105
Loading type: uniform loading across the plates
Edge boundary condition: simply supported
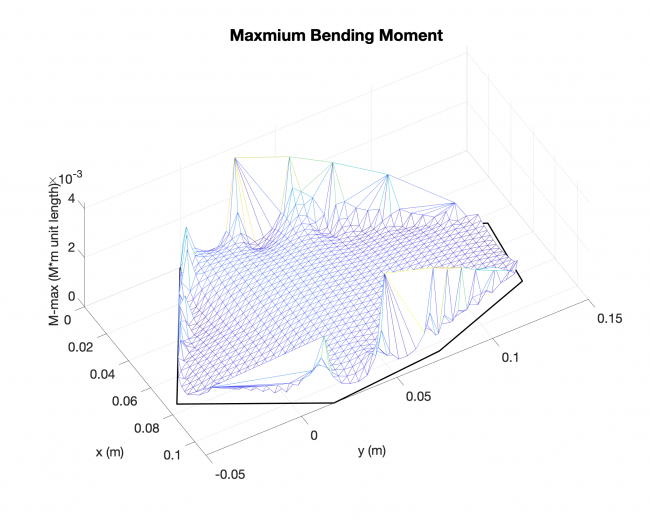
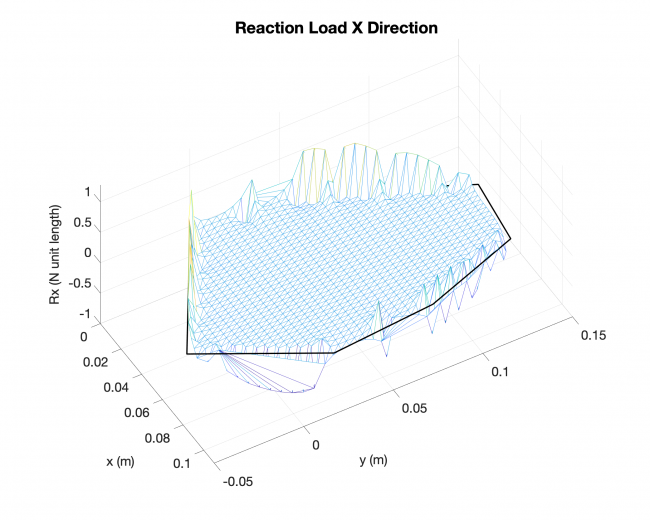
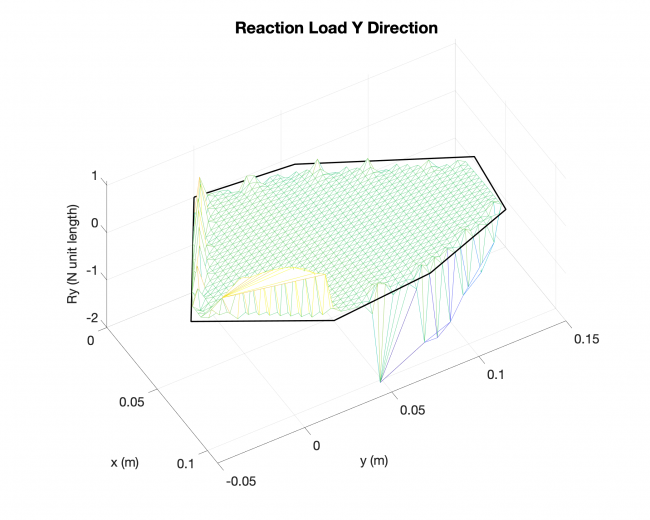
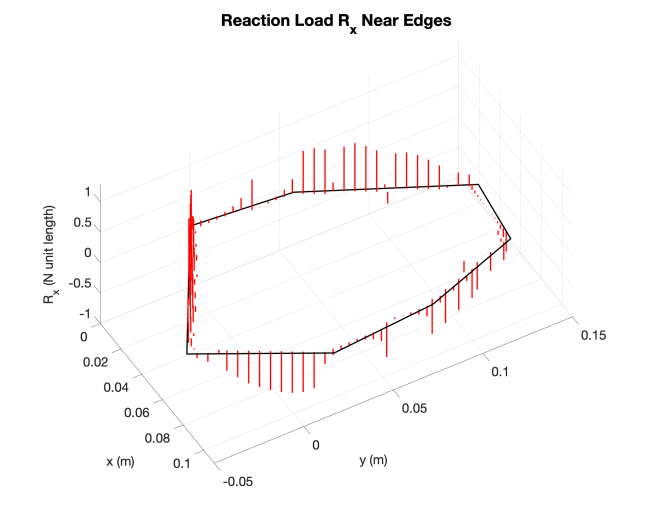
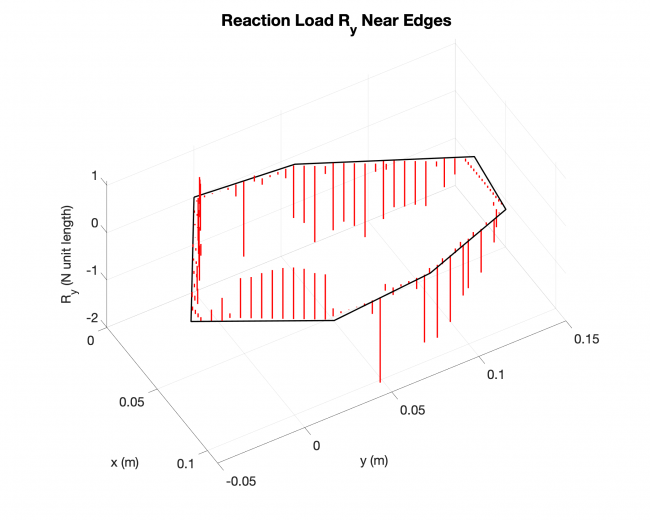
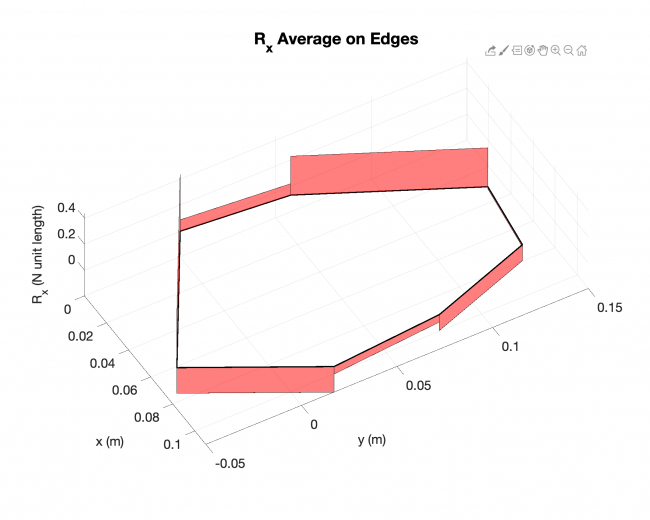
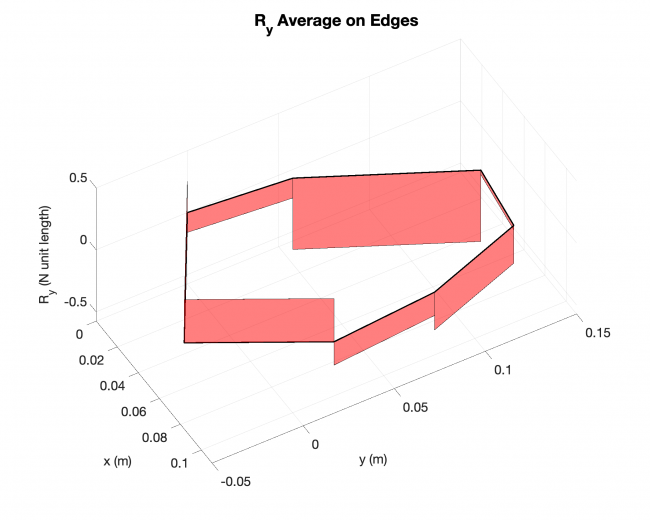
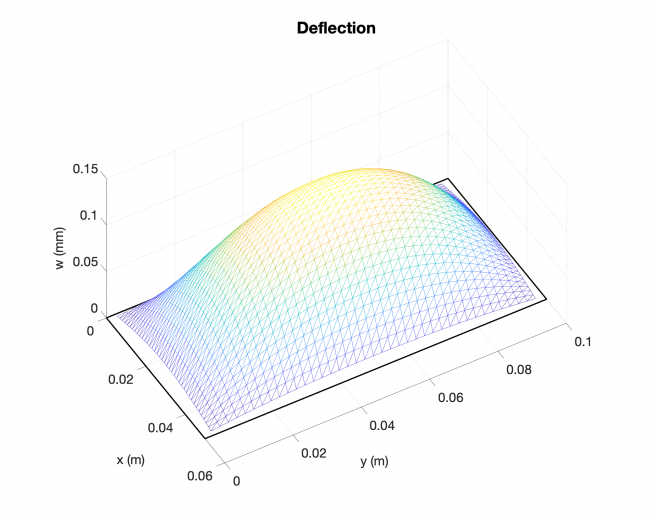
A simple validation: Linearized solution V.S. Analytical solution, rectangular plate
Number of edges: 4
Loading type: uniform loading across the plates
Edge boundary condition: simply supported
--------------------- Linearized solution ------------------------------ Analytical solution ----------------
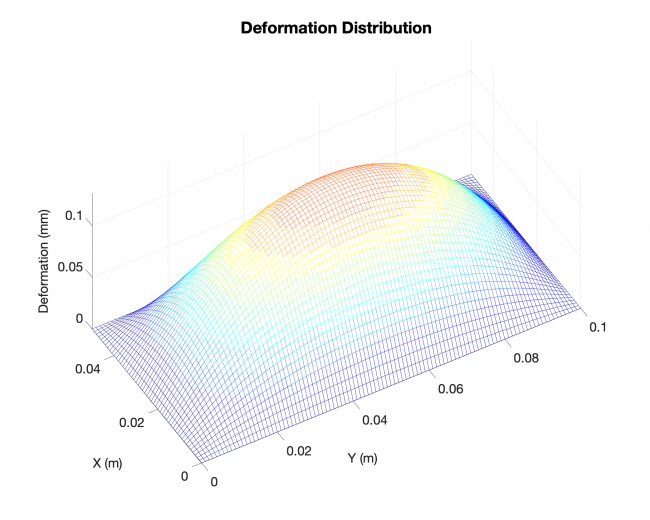
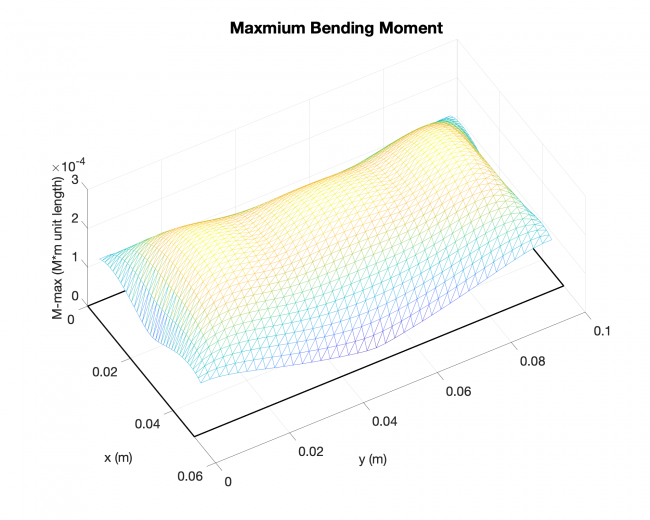
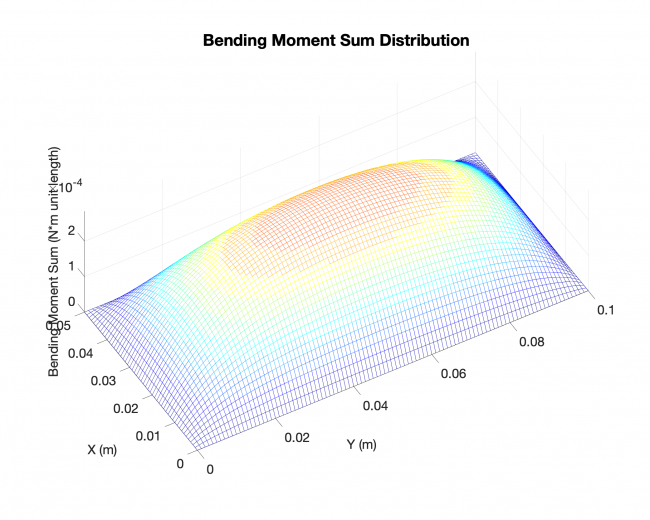
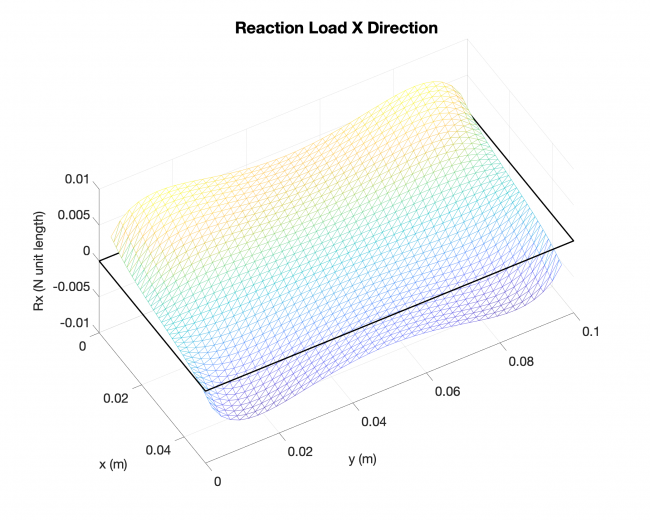
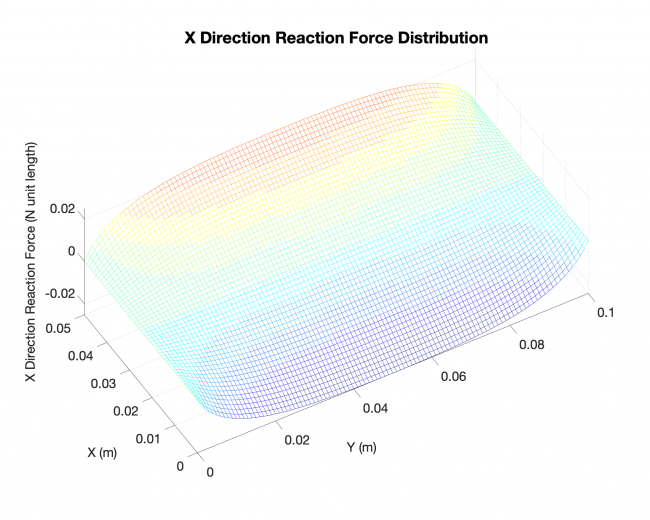
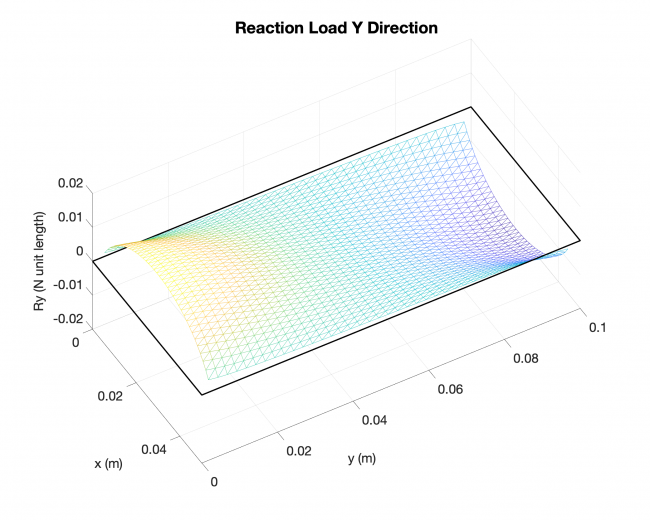
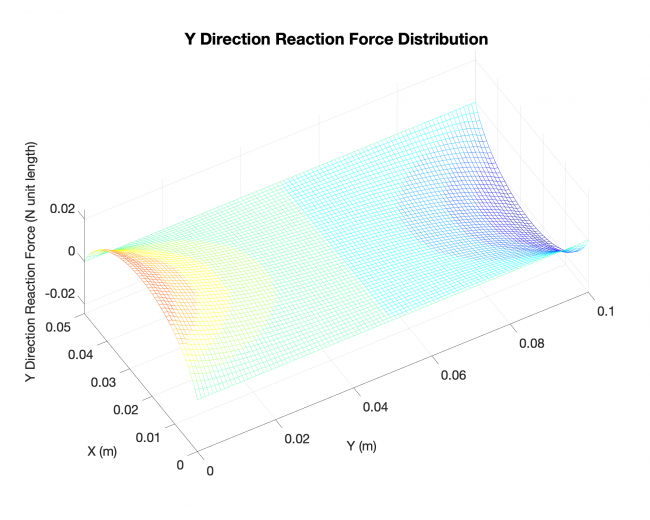
Future work for next week
1. Solve edge problem
2. Different loading conditions
3. Different boundary conditions
Appendix: Linearization of plate theory. Derivation as shown below.
Please let me know if you find any typos. Thanks.






