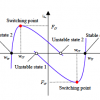
Based on what happened in the experiments, we found that there may be some other definitions of snap-through other than reaching the critical switching point, depending on whether the system is under force control or displacement control. For this reason, new model of the mechanical logic system mig...

Last quarter I finished building the model of the oscillation period of the mechanical logic in one single snap-through motion. This week I studied the periodic motion of the system and found that as the oscillation becomes stable, the oscillation period tends to decrease over time before converging...

Under Dr.Mehta's suggestion, I enhanced my approach to my optimization problem with the use of fmincon in Matlab. The completion of this task marks the start of our writing stage.

This week I redesigned an algorithm that calculates design parameters of the mechanical logic this week. Given that there are so many degrees of freedom, we need to find something to optimize and thus determine the best possible combination of parameters. One thing to optimize is the robustness--if...

This week I wrote codes that can help design the bistable beam-CSCP actuator system under certain contraints (e.g. oscillation frequency). The way my codes work reflects my flowchart last week. Since there are a lot of possible combinations of design parameters that may make the mechanical logic o...

I wrote an algorithm that can calculate the optimal design parameters of a bistable buckled beam under some given constraints. The calculated parameters are expected to not only satisfy the constraints, but also make designing easy.

At the same time I worked on modeling the critical force and critical displacement of the bistable beam, I also looked into the way these behavioral parameters affected the final output parameter of the system--the oscillation period of the mechanical logic. I integrated the models for the mechanica...

Due to the shortcomings of the ROM (it's really hard to translate into our fast, model-based design method for the mechanical logic), I have started to work with a new model that we used for the ISER paper (it turned out more than a piecewise linear model that came to the rescue at that time). This...

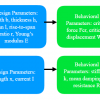
As I mentioned in the group meeting last Thursday, to better communicate what I have been doing with the modeling of one subsystem of the mechanical logic, I am writing up and summarizing my progress up until now. I included some pics from my writeup, but the full pdf will soon be on my personal pag...

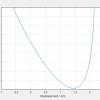
Here is the cubic force-displacement curve obtained after I adjusted the parameters / coefficients based on the results from our experiment.