Currently working on the first step of a simulation for Tsang-Kai's SLAM project. A simulation will help verify landmark accuracy among other things beyond what can be demostrated using datasets. Ultimately we would like the simulation to look like the below figure [1] .
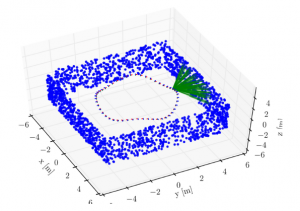
The simulation setup above has the IMU and camera moving in a circular trajectory while observing features (green lines) on the walls of the square environment. The simulation will be used to compare optimization-based NLS SLAM to the filtering-based EM SLAM and Block Online EM SLAM. Generalized coordinates are position, velocity, orientation.
TODO: Using methods similar to [2], we first build the circular trajectory. Then we input the body's acceleration and angular velocity to the following equations to get the accelerometer and gyroscope readout:
\(y_{a,t} = R_t^{bn}(a_n^{nn} - g^n) + \delta_{a,t}^b + e_{a,t}^b\)
\(y_{w,t} = \omega_{nb,t}^b + \delta_{w,t}^b + e_{w,t}^b\),
where we assume the bias term (\(\delta\)) is zero and the noise (e) is zero mean Gaussian. This is part of the data given to the SLAM algorithms.
TOCHECK: Integrate IMU data to obtain position/velocity/orientation:
\(p_{t+1}^n = p_t^n + Tv_t^n + \frac{T^2}{2}( R_t^{bn}(y_{a,t} - \delta_{a,t}) + g^n + e_{a,t})\),
\(v_{t+1}^n = v_t^n + T( R_t^{bn}(y_{a,t} - \delta_{a,t}) + g^n + e_{a,t})\),
\(q_{t+1}^{nb} = q_t^{nb}\bigodot exp_q(\frac{T}{2}(y_{w,t} - \delta_{w,t} - e_{w,t}))\).
We treat the above equations as observations (dead reckoning) so the noise terms are equal to zero. First input IMU data without sensor noise to try to get a trajectory very close to the original (noise from integration still occurs).
CHALLENGES: I'm not very familiar with c++, which is the major hurdle in all of this. I need to become more comfortable with quaternions and the Eigen library [3]. Things like syntax, memory management, and data handling are important to understand. Much of what I need is already coded so it shouldn't be an impossible task.