During the past week, I have been doing background study on plate theory. The short term goal is to be able to determine plate behavior when applied loads. The long term goal is to be able to determine behavior of arbitrary foldable structures (which are assembled with plates), with different boundary conditions, and under arbitrary loading conditions.

Introduction

We would like to design foldable origami structures based on behavioral specifications. The first step is to get to know where will the structure fail, without actually building one.

My approach: when having a foldable pattern what can be folded into a cuboid (with six rectangular plates), we will study each plate under load individually.

In order to do so, I will need to have basic understanding of plate theory.

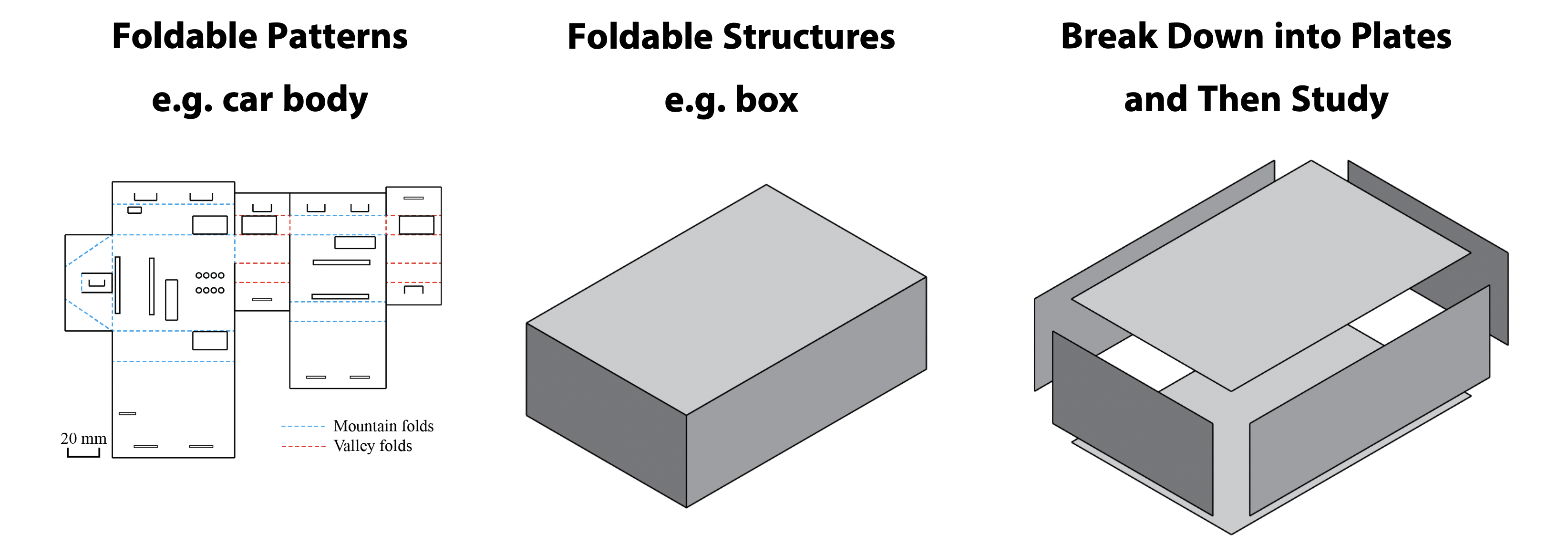
Background Information

Plate Theory

Basic plate theory is presented below.

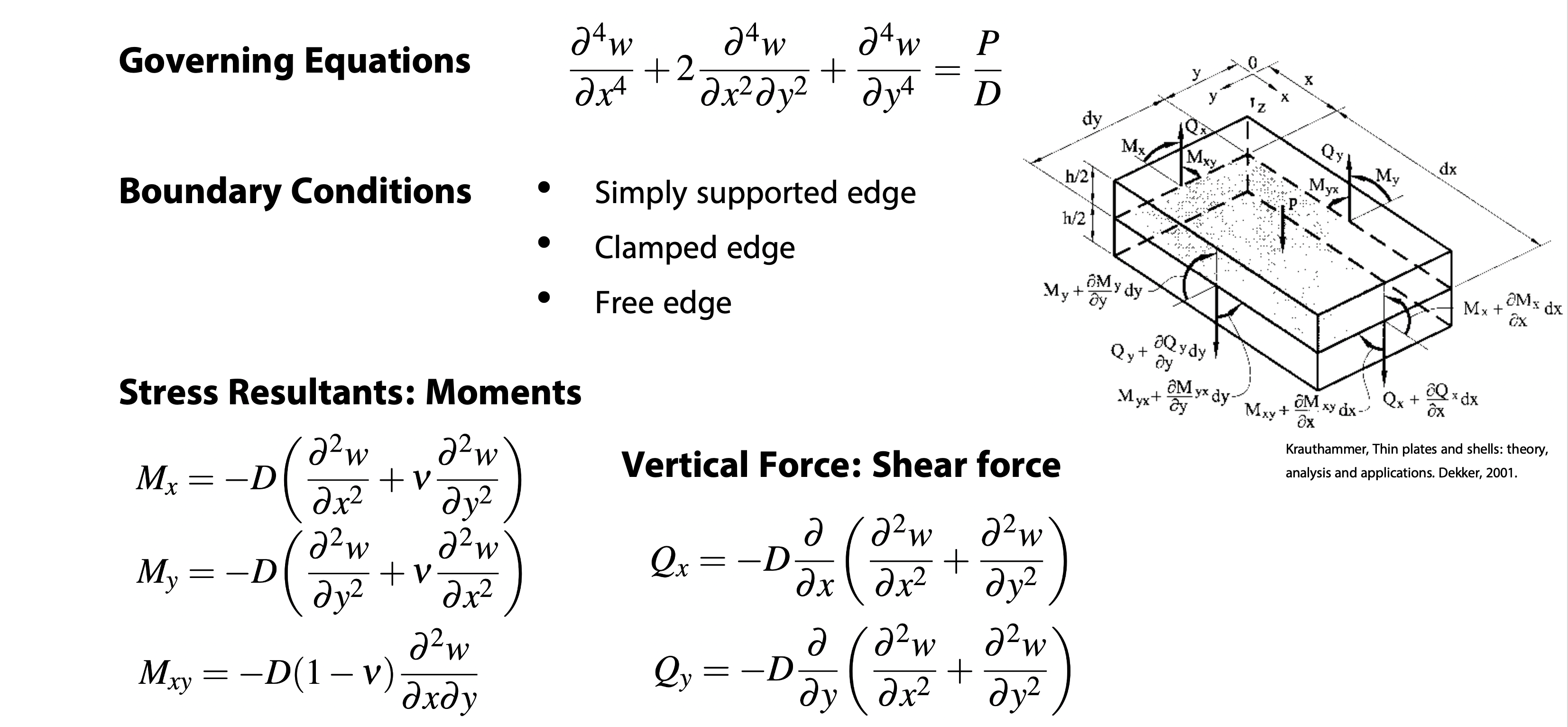
Example

The challenging part is to solve the governing equation under different boundary conditions. I have done some literature review and found some analyical solutions for certain conditions. But more need to be done.

For now, I will use some examples to validate the workflow I have in my mind (how I plan to get the weak point and failure mode in this foldable structure using classical plate theory).

The workflow is presented below using two examples.

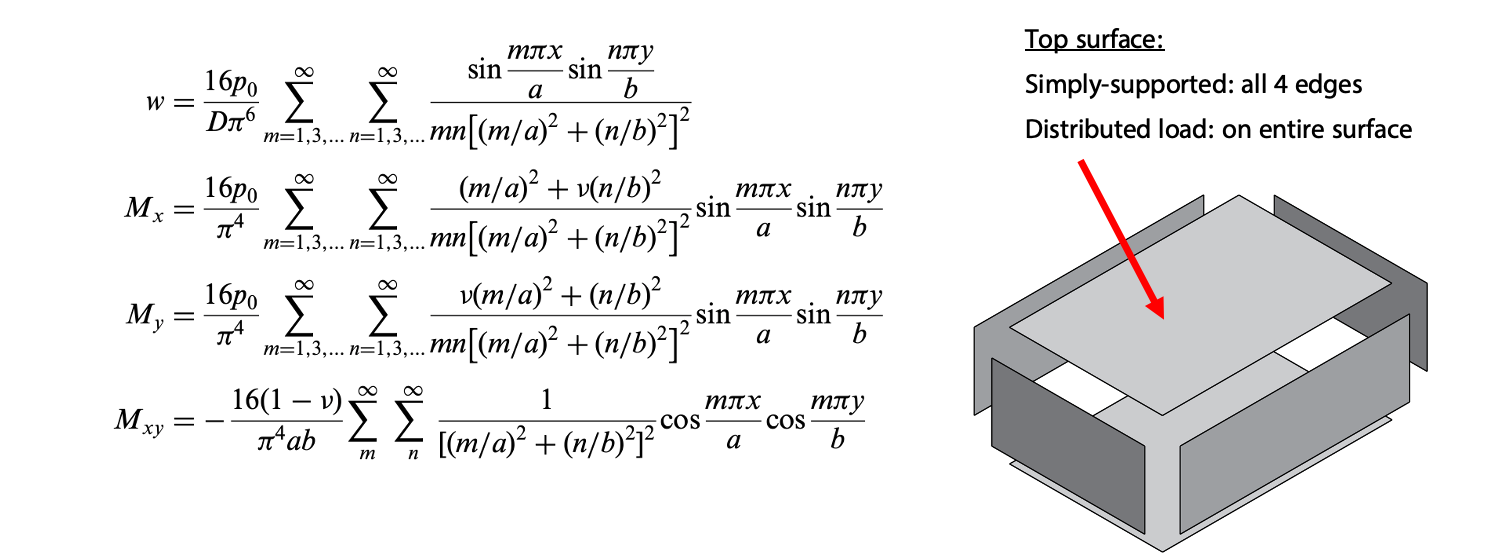
Example: Simply Supported on All 4 Edges, Distrubuted Load on Top Plate

The following results are for top plate, which is under load.

Analytical Solutions (Well-Defined in Literature and Textbooks)

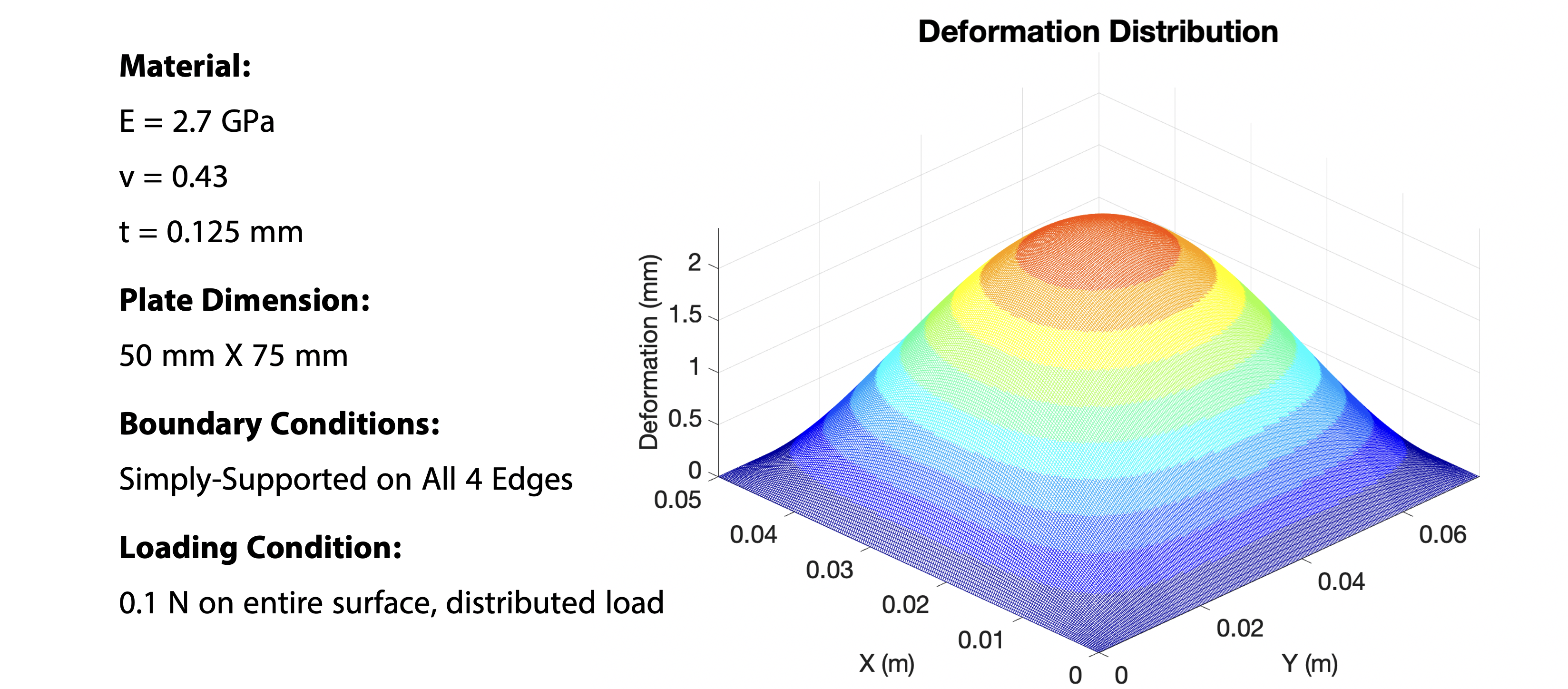
System Parameters and {Loading Plate} Deformation Distrubution

The deformation distrubution can tell us what is the maximum deformation and how much it is. The value can be used to compare with behavioral specification (if any).

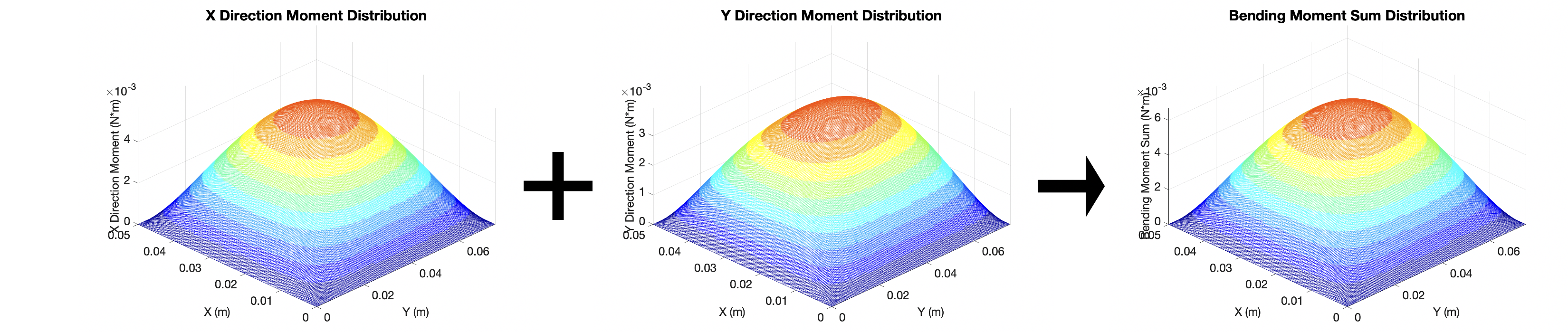
{Loading Plate} Bending Moment Distrubution

The bending moment can be used to calculate bending stress in the plates. The value can be used to compare with behavioral specification (if any).

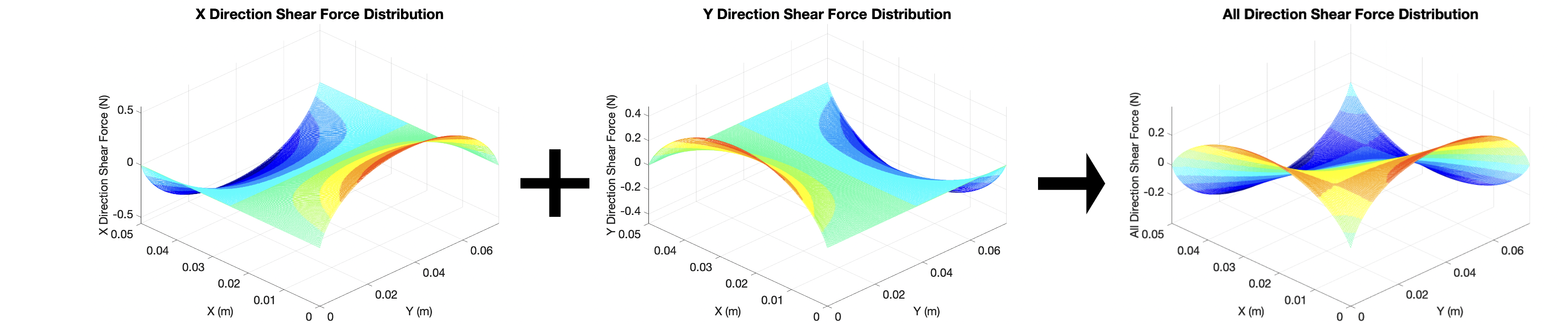
{Loading Plate} Shear Force Distrubution

The value can be used to compare with behavioral specification (if any).

Load "Transition"

To transfer load applied to the top plates to the other plates, bending moment at edges and shear force at edges are used (here all edges are simply supported, therefore bending moments at all edges are zero).

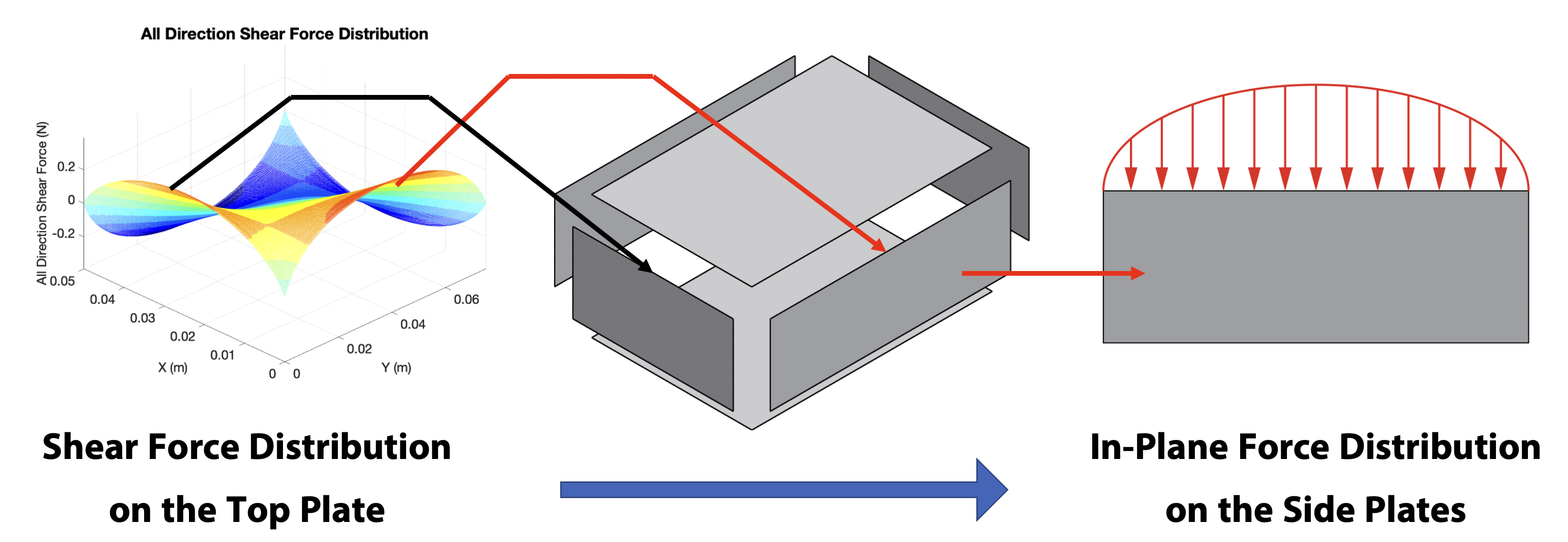
{Other Plates} Deformation Distribution, Bending Moment and Shear Force

To-be-continued

Challenges

--- Lack of solved (ready-to-use) equations for different loading & boundary conditions. This will make it hard to keep using this plate theory.

--- However, the workflow should be the same. AKA, starting from the loading plate, solving each plate individually. Then using force & moment one the edges for other plates.

--- A potential solution is to simplify each plate as bar-hinge truss structure. Using MATLAB programmable FEA to solve this problem.

--- This simplified FEA version can be suitable since it will/may be easier to define loading functions (will be concentated force on each node) and boundary conditions (will be loading conditions on each node).

--- Easy to adopt to arbitrary shapes, not limited to rectangular plates.

For the Coming Week

--- Background study on basic FEA theory (should be quick since I took the class before).

--- Research on 3D FEA theory (I don't know if we can apply load to nodes at random orientation, yet. But my guess is we can, which will be helpful).

--- Program plate bending with arbitrary loading conditions and boundary conditions using MATLAB.

Next Post Previous Post