06 Apr

Computational Design of Planar 3D Structures -- Buckling -- Intermedium Results

Chang Liu origami robots

There are three steps I will take in order to implement this design tool:

Step 1: Verify I operate correctly in FEA (Solidworks Simulation). In order to do this, I will use some existing numerical solution and/or analytical solutions to find out critical buckling load. Then I will apply this critical buckling load to FEA analysis. If the resulting buckling factor (called safety factor in Solidworks Simulation) equals to 1, it means results from existing solutions match FEA result. Then I will continue to the next step.

Step 2: Develop and evaluate plane stress. We first need to convert loads on edges to stress distributed in plane. Plane stress analysis in our design tool will result in stress distribution (von mises stress) in plates under in-plane loads. In FEA, I will conduct static analysis with in-plane loading. Stress results will be used to compare with that obtained using our design tool. If results match, or at the same magnitude, or have the same trend, I will continue to the next step.

Step 3: Develop and evaluate plate buckling. Stress distribution from step 2 will be used to calculate work load energy in buckling analysis, in order to be used on principle of minimum potential energy calculation. The buckling analysis will be implemented in my design tool, and converted into an eigenvalue problem. The eigenvalue will be the buckling factor. If it is greater than 1, it means no buckling happens in plate; if it is small then 1, it means the plate buckles; and if it is 1, it means we just find critical buckling load. This buckling factor will be compared with that obtained from FEA buckling analysis. If they match, it means this subproblem has been satisfactorily solved.

Step 1: Verify FEA operations using existing analytical approach

I tried to verify my FEA operation using the following steps:

  • Find out existing analytical solutions and numerical solutions. I decide to use 5 examples, as presented below.
  • Calculate theortical critical buckling load from those solutions.
  • Build models in Solidworks Simulation, apply correct boundary and loading conditions.
  • Run buckling analysis, check results (safety buckling factor).
Example 1: SSSS
  • Shape and dimension: rectangular 100mm x 50mm x 1mm plate
  • Boundary condition: simply supported on all four edges
  • Loading condition: uniaxial compression on shorter edges
  • Mechanical properties: E = 3GPa, v = 0.25
  • Critical buckling load from analytical solutions: 4212N/m along the short edges, or 210N on short edges or 84240 N/m^2 on short edges. Also there should be two half-waves across lengthwise direction and one half-wave along widthwise direction.
  • FEA result: buckling factor of safety = 1.0095. Results can be found bellow:

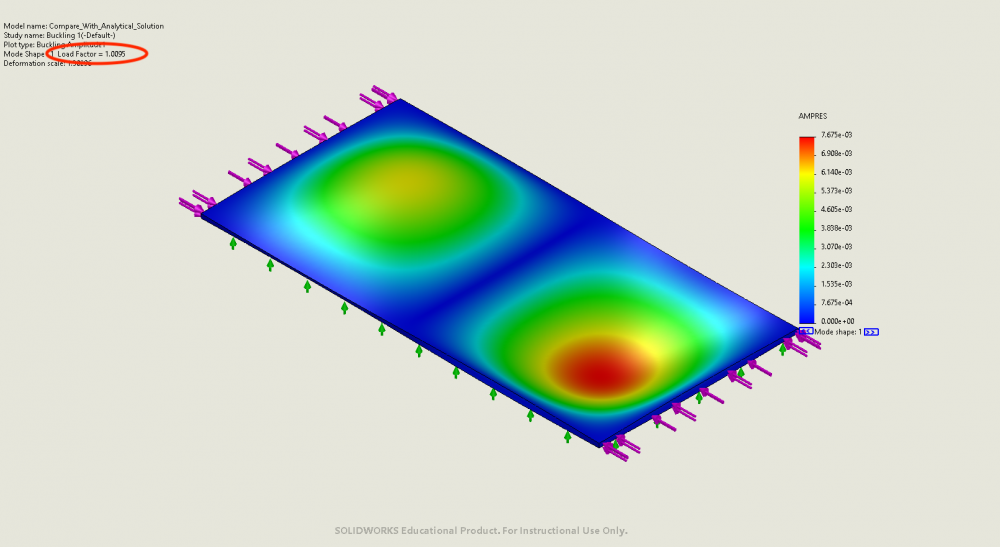
Example 2: SCSC
  • Shape and dimension: rectangular 100mm x 50mm x 1mm plate
  • Boundary condition: simply supported on two short edges, fixed on two long edges
  • Loading condition: uniaxial compression on shorter edges
  • Mechanical properties: E = 3GPa, v = 0.25
  • Critical buckling load from analytical solutions: 7340N/m along the short edges, or 367N on short edges.
  • FEA result: buckling factor of safety = 1.025. Results can be found bellow:

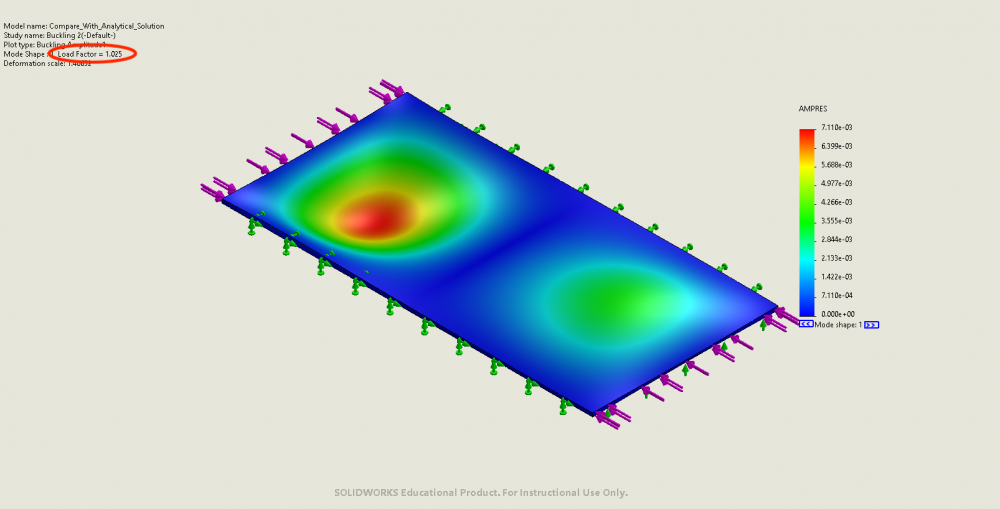
Example 3: SFSF
  • Shape and dimension: rectangular 100mm x 50mm x 1mm plate
  • Boundary condition: simply supported on two short edges, free on the two long edges
  • Loading condition: uniaxial compression on shorter edges
  • Mechanical properties: E = 3GPa, v = 0.25
  • Critical buckling load from analytical solutions: 13.16N on short edges.
  • FEA result: buckling factor of safety = 0.95. Results can be found bellow:

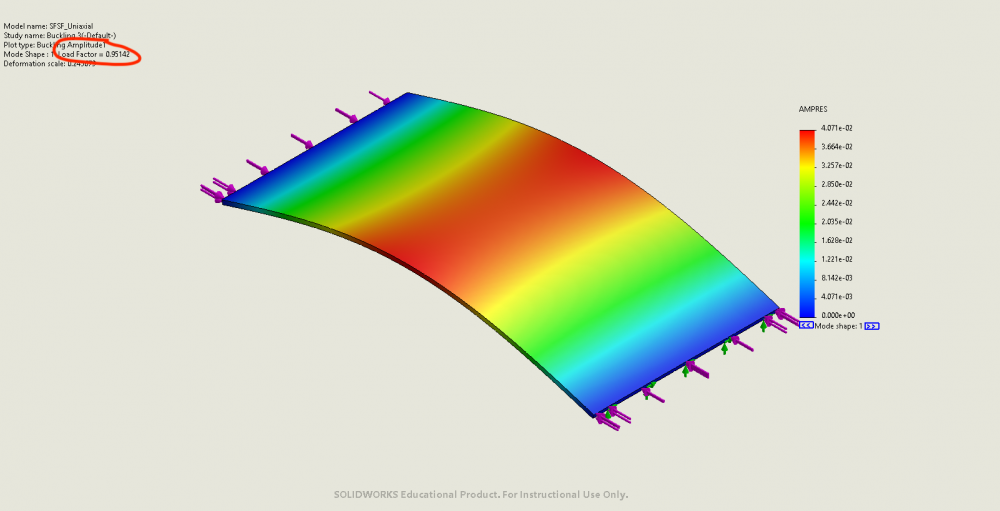
Example 4: SFCF
  • Shape and dimension: rectangular 100mm x 50mm x 1mm plate
  • Boundary condition: simply supported on one short edge, fixed on the other, free on the two long edges
  • Loading condition: uniaxial compression on shorter edges
  • Mechanical properties: E = 3GPa, v = 0.25
  • Critical buckling load from analytical solutions: 26.3N on short edges.
  • FEA result: buckling factor of safety = 0.9884. Results can be found bellow:

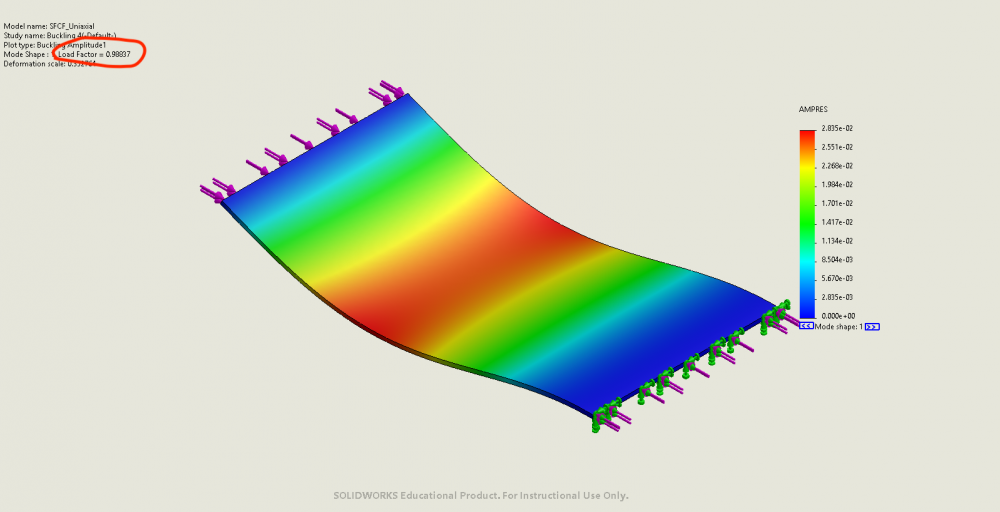
Example 5: CFFF
  • Shape and dimension: rectangular 100mm x 50mm x 1mm plate
  • Boundary condition: fixed on one short edge, free on the other three edges
  • Loading condition: uniaxial compression on shorter edges
  • Mechanical properties: E = 3GPa, v = 0.25
  • Critical buckling load from analytical solutions: 3.29N on short edges.
  • FEA result: buckling factor of safety = 0.9610. Results can be found bellow:

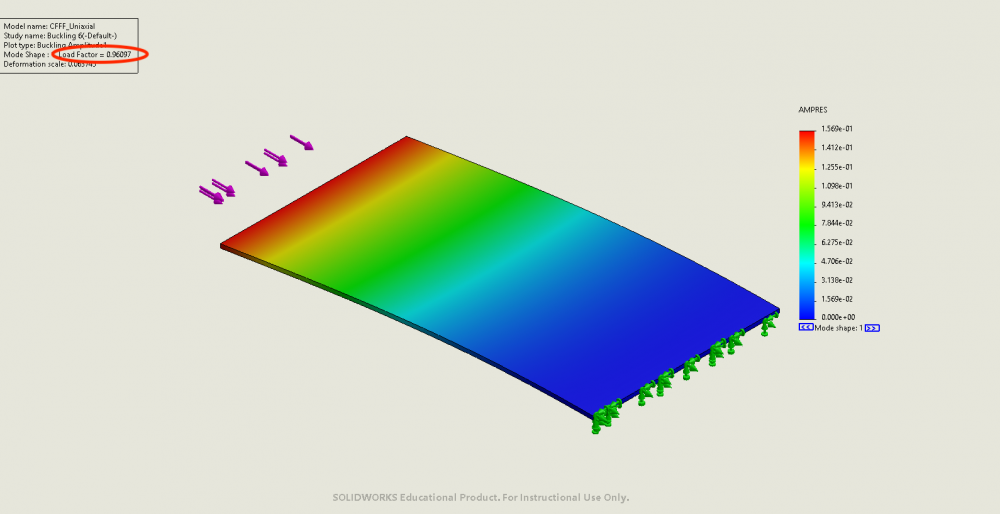
These five cases have been verified. These five cases will be used to verify plane stress results in the next step.

Step 2: verify plane stress analysis in our design tool

Same examples are used, with the following parameters:

  • Shape and dimension: rectangular 100mm x 50mm x 1mm plate
  • Loading condition: uniaxial compression on shorter edges
  • Mechanical properties: E = 3GPa, v = 0.25
Example 1: SSSS
  • Boundary condition: simply supported on all four edges
  • Critical buckling load from analytical solutions: 210N on short edges
  • FEA stress analysis results:

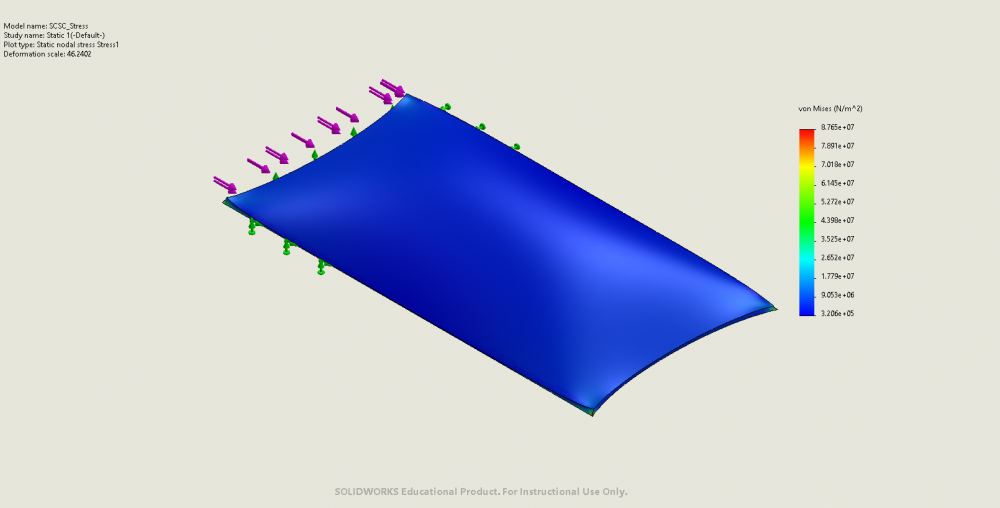
Example 2: SCSC
  • Boundary condition: simply supported on two short edges, fixed on two long edges
  • Critical buckling load from analytical solutions: 367N on short edges
  • FEA stress analysis results:

Example 3: SFSF
  • Boundary condition: simply supported on two short edges, free on the two long edges
  • Critical buckling load from analytical solutions: 13.16N on short edges
  • FEA stress analysis results:

Example 4: SFCF
  • Boundary condition: simply supported on one short edge, fixed on the other, free on the two long edges
  • Critical buckling load from analytical solutions: 26.3N on short edges
  • FEA stress analysis results:

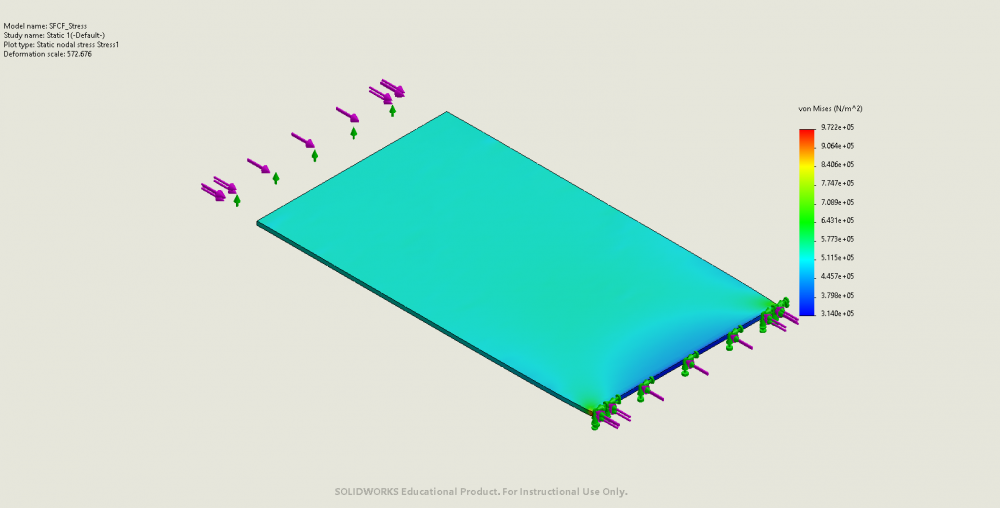
Example 5: CFFF
  • Boundary condition: fixed on one short edge, free on the other three edges
  • Critical buckling load from analytical solutions: 52.6N on short edges
  • FEA stress analysis results:

Next Post Previous Post

Search

Popular Tags

foray origami robots blimp ducky vr edg SLAM computer vision computational design roco slam Origami rocolib arduino RoCo design Robot Compiler simulation Motion Planning autonomy edg-model mesh reinforcement learning; multi-agent; mean-field; logics create; kalman filter; motors imu friction mesh network tank esp32 networking contacts multi-agent pushing auxetic machine learning dynamics esp now visual processing wireless control communication webapp pcbs structure ROCO i2c path planning cars Robotica reinforcement learning computer skill openmv test motor dataset visual DARPA odometry Battery surface structure power consumption dash port-arrays modeling origami paper frequency diversity semantic infrastructure auxetics feedback gondola machine vision Consensus bistable auxetic controller gestural intuition mixed reality unit cell robot crawler gestural interface open house network create; kalman filter; EM; refactoring 4-wheeled darpa; create; icra2021 apriltags lidar logic control FORAY perception Quantum Information crazyflie 433mhz optimization propeller Foray structures sensors environmental design radio DER Kullback-Leibler Divergence lasercutter tutorial von Mises Fisher Distribution IR simulink legs project management localization distributed optimization blynk Auxetics painlessmesh experiment results offline reinforcement learning exam research proposal altimeter thrust PCB sensor fusion gate or webots multi-agent path planning UAV RL integration test arnhold joystick balloon test vision processing pushing problem modeling contacts mesh networking motor configuration nodemcu swarm object detection fusionbot ros2 rviz2 gazebo conference matlab arduino nano decentralized surfaces keyboard IROS Integrated Demo throughput peripheral device paper review reinforcement learning; motorized boats Writing slam; paper review rhino Short Post range distance surp origami robot nylon pvdf elastic polymers plastic hot plates reinforcement learning; multi-agent; mean-field; game theory; mean field; reinforcement learning current reinforcement learning; multi-agent; Xbee Zigbee robot compiler spi contact neural network dynamic modeling quasi-static modeling edg-examples Kalman Filter port-array von Mises Fisher von Mises-Fisher literature review multipack car Zero Elastic Energy modes swarm control solar cars system ID serial monitor edg-ide Discrete Elastic Rods ceres debug Consensus Algorithms coriolis force dynamic model proposal wtf deep learning pdms interpolation wireless signal strength reinforcement learning; multi-agent; decentralized misc reinforcement learning; multi-agent; mean-field; stationary demo video flytrap papers steering structured field pivoting differential power detectionrate color shape edg-refactoring pain python vision Machine Learning Q-Learning Model-Free release conferences quasi-static pushing liquid crystal elastomer nonholonomic systems iot grant feedback-controlled controls trajectory optimization surface contact Characterization tool ML multi-agent path finding Liquid Crystal Elastomers Learning kinematic_model reservoir computing 2.4 GHz concept 433 MHz Bayesian Network creative Computer skill internal silicone integrated system instance segmentation marginal cost pricing bootstrapping Bayesian networks ensemble methods offline Rl hardware manipulation COVID 19 paper cutter ESP32 kalman filter; multi-robot state space delta tolling buoyancy chiral square unit cell pressure distribution model prediction thrust configuration grid fabrication firmware protobuf #activecapturingmechanism #claw 3D-CHESS; kalman filter boxboat tracking model-based RL von Mises Distribution slam; flowchart; spring-mass 3D-CHESS; 433 rssi signal strength multirobot system writing in-situ design buoyancy equations boat deployment cell cameras der newton's method Barycenter Euler-Bernoulli beam sma-based actuator game theory Bessel functions von Mises-Fisher Distributions ide HDL board design battery current sensor ZMP center of friction Multi-Agent Systems code balloon semantic segmentation MIMO communications ICRA ICML guassian processes probabilistic neural networks graph generators MBRL batch learning ros edg-compiler multirobot optitrack adaptive control motor driver submission DNN kalman filtering point cloud 2.4ghz latency scenic codesign presentations machine training preliminary exam multiple devices inkscape material multi-object tracking ICLR Python actuation catching mechanism integration flapping color_segmentation lab_data result segmentation on multiple object and centers finding competition prelab multiple blimps pid defender Synthesizable Radio 3d printing kalman filter motor distribution barometer detection lift force depth estimation cad solidworks design tool pixracer pixhawk ardupilot flight controller regression fly test sensor selection