11 Apr

von Mises Fisher Distributions in Quantum Information

Cody Fan von Mises Fisher Quantum Information

Last month Tsang-Kai emailed me his proof for the solution for KL Average for von Mises-Fisher distributions. Now we are looking for ways in which we can apply this to different real engineering problems that exist.

One interesting application of von Mises-Fisher distributions is in Quantum Information theory. One way to represent a quantum state is by a bloch sphere 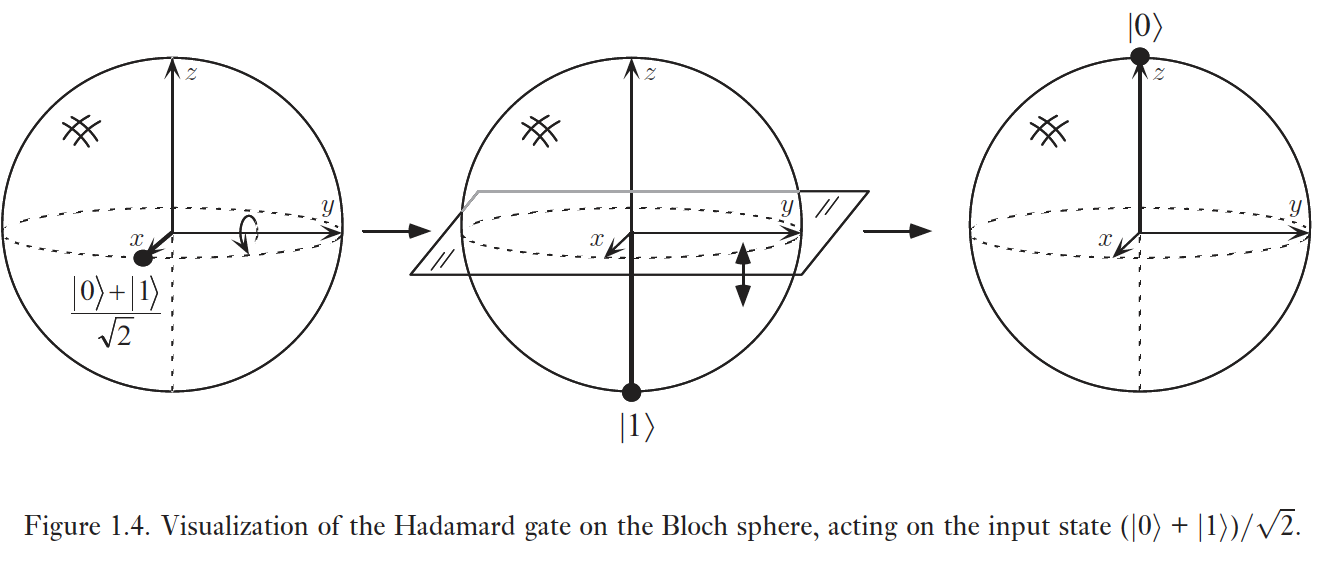[Nielsen and Chuang, 2010].

However, in practice one cannot clone a Quantum State as a result of the no cloning theorem, and direct measurement of a quantum state will collapse it to one of the computational basis states of the measurement. Enter Quantum Tomography, were one tries to estimate the state of a qubit. Since the state of a qubit can be represented on a sphere, one idea that has come to the field of Quantum Information theory is to use directional statistics for the representation of Quantum States, mentioned in [Shultz, 2016]. In fact, he mentioned that we can use the von Mises-Fisher distribution to represent random pure states and that we can use the Bingham distribution to represent random mixed states. Also mentioned was the usage of matrix versions of these distributions to represent unitary operations on states. In his paper Shultz utilizes Choi matricies in conjuction with von Mises-Fisher class of distributions to Dephase noise, and Bingham type distributions to Depolarize noise. Also, some researchers suggest that von Mises-Fisher distributions are useful for preparing initial pure states (before computations occur) Wudarski et al. 2020].

Also interesting and related is the field of Quantum Consensus. Most of the current work is reviewed in Marcozzi and Mostarda, 2021]. Most of the current work seems to be on the straight up qubit representation of quantum states (without any fancy distributions involved).

One idea could be to use consensus of von Mises-Fisher distributions as a method to prepare the initial pure states of a Quantum network if we wish to have the quantum network be initialized from a state of consensus!

Next Post Previous Post

Search

Popular Tags

foray origami robots blimp ducky vr edg SLAM computer vision computational design roco slam Origami rocolib arduino RoCo design Robot Compiler simulation Motion Planning autonomy edg-model mesh reinforcement learning; multi-agent; mean-field; logics create; kalman filter; motors imu friction mesh network tank esp32 networking contacts multi-agent pushing auxetic machine learning dynamics esp now visual processing wireless control communication webapp pcbs structure ROCO i2c path planning cars Robotica reinforcement learning computer skill openmv test motor dataset visual DARPA odometry Battery surface structure power consumption dash port-arrays modeling origami paper frequency diversity semantic infrastructure auxetics feedback gondola machine vision Consensus bistable auxetic controller gestural intuition mixed reality unit cell robot crawler gestural interface open house network create; kalman filter; EM; refactoring 4-wheeled darpa; create; icra2021 apriltags lidar logic control FORAY perception Quantum Information crazyflie 433mhz optimization propeller Foray structures sensors environmental design radio DER Kullback-Leibler Divergence lasercutter tutorial von Mises Fisher Distribution IR simulink legs project management localization distributed optimization blynk Auxetics painlessmesh experiment results offline reinforcement learning exam research proposal altimeter thrust PCB sensor fusion gate or webots multi-agent path planning UAV RL integration test arnhold joystick balloon test vision processing pushing problem modeling contacts mesh networking motor configuration nodemcu swarm object detection fusionbot ros2 rviz2 gazebo conference matlab arduino nano decentralized surfaces keyboard IROS Integrated Demo throughput peripheral device paper review reinforcement learning; motorized boats Writing slam; paper review rhino Short Post range distance surp origami robot nylon pvdf elastic polymers plastic hot plates reinforcement learning; multi-agent; mean-field; game theory; mean field; reinforcement learning current reinforcement learning; multi-agent; Xbee Zigbee robot compiler spi contact neural network dynamic modeling quasi-static modeling edg-examples Kalman Filter port-array von Mises Fisher von Mises-Fisher literature review multipack car Zero Elastic Energy modes swarm control solar cars system ID serial monitor edg-ide Discrete Elastic Rods ceres debug Consensus Algorithms coriolis force dynamic model proposal wtf deep learning pdms interpolation wireless signal strength reinforcement learning; multi-agent; decentralized misc reinforcement learning; multi-agent; mean-field; stationary demo video flytrap papers steering structured field pivoting differential power detectionrate color shape edg-refactoring pain python vision Machine Learning Q-Learning Model-Free release conferences quasi-static pushing liquid crystal elastomer nonholonomic systems iot grant feedback-controlled controls trajectory optimization surface contact Characterization tool ML multi-agent path finding Liquid Crystal Elastomers Learning kinematic_model reservoir computing 2.4 GHz concept 433 MHz Bayesian Network creative Computer skill internal silicone integrated system instance segmentation marginal cost pricing bootstrapping Bayesian networks ensemble methods offline Rl hardware manipulation COVID 19 paper cutter ESP32 kalman filter; multi-robot state space delta tolling buoyancy chiral square unit cell pressure distribution model prediction thrust configuration grid fabrication firmware protobuf #activecapturingmechanism #claw 3D-CHESS; kalman filter boxboat tracking model-based RL von Mises Distribution slam; flowchart; spring-mass 3D-CHESS; 433 rssi signal strength multirobot system writing in-situ design buoyancy equations boat deployment cell cameras der newton's method Barycenter Euler-Bernoulli beam sma-based actuator game theory Bessel functions von Mises-Fisher Distributions ide HDL board design battery current sensor ZMP center of friction Multi-Agent Systems code balloon semantic segmentation MIMO communications ICRA ICML guassian processes probabilistic neural networks graph generators MBRL batch learning ros edg-compiler multirobot optitrack adaptive control motor driver submission DNN kalman filtering point cloud 2.4ghz latency scenic codesign presentations machine training preliminary exam multiple devices inkscape material multi-object tracking ICLR Python actuation catching mechanism integration flapping color_segmentation lab_data result segmentation on multiple object and centers finding competition prelab multiple blimps pid defender Synthesizable Radio 3d printing kalman filter motor distribution barometer detection lift force depth estimation cad solidworks design tool pixracer pixhawk ardupilot flight controller regression fly test sensor selection