Distributed estimation and robotic localization

Information exchange and fusion is essential to the success of multirobot systems

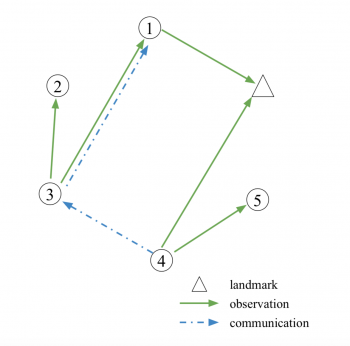
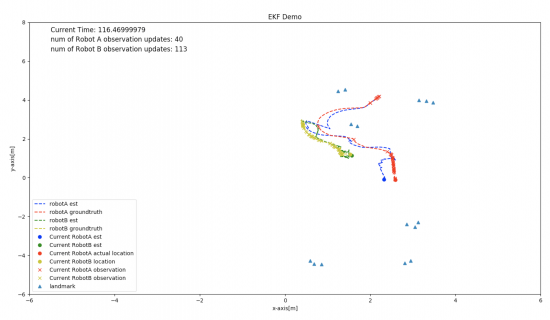
We utilize Kalman filter with covariance intersection for the distributed estimation problem, where estimation consistency is guaranteed throughout the process. In the theoretical persepctive, we show that covariance intersection decreases the unobservable space of the equivalent state-space model, and therefore the boundedness criterion is relaxed. In application, the distributed estimation algorithm is successfully applied on multirobot cooperative localization. In this scenarion, the communication can be separated as an independent step in the localization algorithm, which facilitates further operation-cost optimization in reality.

We also research other recursive Bayesian-based distributed state estimation algorithms such as variants on the von Mises filter to ensure estimation consistency in tracking orientation. As a part of this research, we also look into the Consensus problem on various families of distributions, such as von Mises-Fisher, Bingham, and more.